Volume rendering should consider not only the interaction between light and object surface, but also the interaction with a large number of particles in space. In this article, the general theory of volume rendering is introduced, and the ray propagation equation in the form of integral equation is derived. Finally, an example of real-time volume rendering is given.

Volume Media

The volume medium is composed of a large number of particles in the volume. When light propagates in the medium, there may be three situations: transmission, absorption and scattering.

Figure 1 - Interaction of Light Rays with Particles

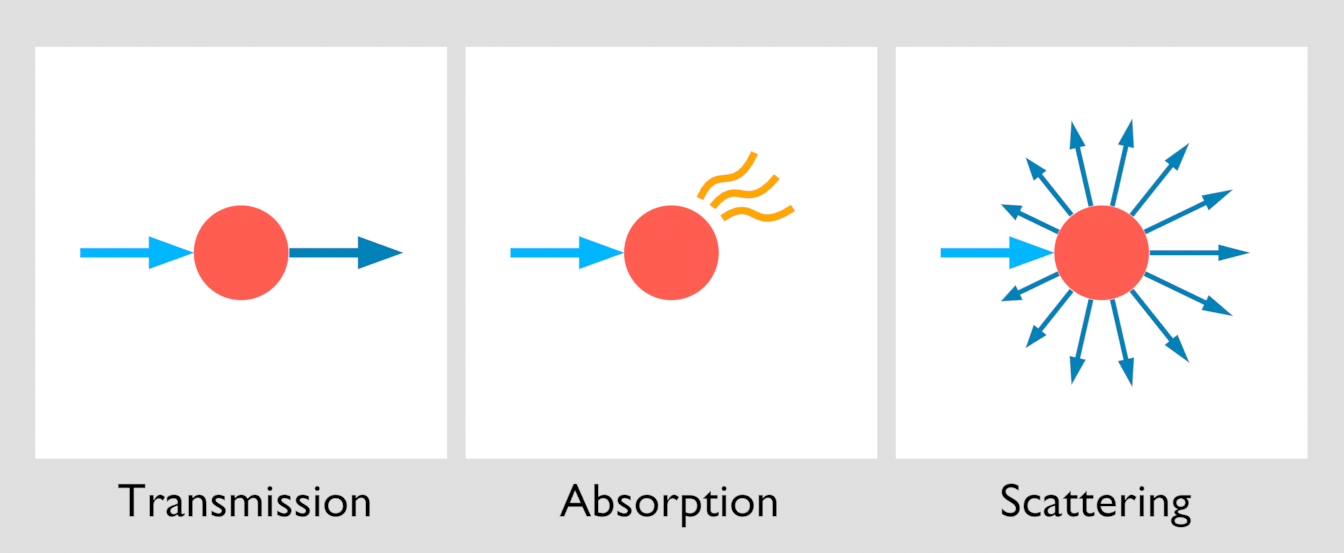
At the same time, there may exist emission in the medium.

Absorption

Absorption is described by the absorption cross section of the medium, usually denoted as $\sigma_a$. Suppose that the light along $\boldsymbol{\omega}$ interacts with the medium at the point $\bf p$. Let $\sigma_a(\mathbf{p},\boldsymbol{\omega})$ be the ratio of the absorbed radiance to the original radiance after the light travels a unit length along the direction of $\boldsymbol{\omega}$ at the point $\bf p$, which can also be understood as the probability of light absorption. If the scattering of light in the medium is not considered, that is, the light always propagates along a straight line, then we can get the following formula about the radiance

$$d L_{o}(\mathbf{p},\boldsymbol{\omega})=-\sigma_{a}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}) d t.$$

Out-scattering

If the light traveling along the direction $\boldsymbol{\omega}$ is scattered to other directions at the point $\bf p$, we call this kind of scattering out-scattering. scattering coefficient $\sigma_s(\mathbf{p},\boldsymbol{\omega})$ represents the ratio of the emissivity scattered by the outside to the original emissivity after the light travels unit length in the direction of $\boldsymbol{\omega}$ at the point $\bf p$. The out-scattering phenomenon is similar to the absorption phenomenon, which will lead to a decrease in the radiance emitted in the direction $\boldsymbol{\omega}$ at the point $\bf p$, denoted by $L_{o}(\mathbf{p},\boldsymbol{\omega})$. The change rate of radiance caused by out-scattering can be described by the following formula

$$\frac{d L_{o}(\mathbf{p},\boldsymbol{\omega})}{d t}=-\sigma_{s}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}).$$

The combined effect of absorption and scattering is called attenuation or extinction. The attenuation coefficient $\sigma_{t}$ is defined as

$$\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})=\sigma_{a}(\mathbf{p},\boldsymbol{\omega})+\sigma_{s}(\mathbf{p},\boldsymbol{\omega}).$$

The attenuation effect can be described by the following equation

$$\frac{d L_{o}(\mathbf{p},\boldsymbol{\omega})}{d t}=-\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}).$$

There are two quantities associated with the attenuation coefficient that are also common. One is the albedo $\rho$, defined as

$$\rho=\frac{\sigma_{s}}{\sigma_{\mathrm{t}}}=\frac{\sigma_{s}}{\sigma_a+\sigma_{s}}.$$

It represents the proportion of scattering effect to the attenuation effect. The other one is the mean free path $1/\sigma_t$, representing the average distance a photon travels along a straight line without being absorbed or scattered.

If only the attenuation effect is considered, then $L_{o}(\mathbf{p},\boldsymbol{\omega})=L_{i}(\mathbf{p},-\boldsymbol{\omega})$, which yields

$$d \ln L_{o}(\mathbf{p},\boldsymbol{\omega})=-\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})dt.$$

Let $\mathbf{p}’=\mathbf{p}+h\boldsymbol{\omega}$, integrating from $\mathbf{p}$ to $\mathbf{p}’$ gives

$$\ln L_{o}(\mathbf{p}',\boldsymbol{\omega})-\ln L_{o}(\mathbf{p},\boldsymbol{\omega})=-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+t \boldsymbol{\omega}, \boldsymbol{\omega}) dt,$$

which leads to

$$T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)=\frac{L_{o}(\mathbf{p}',\boldsymbol{\omega})}{L_{o}(\mathbf{p},\boldsymbol{\omega})}=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+t \boldsymbol{\omega}, \boldsymbol{\omega}) dt}.$$

The term $T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)$ is called beam transmittance, representing the proportion of light rays in a beam that are not absorbed or scattered. $T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)$ has some commonly used properties. One is

$$T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}\right)=1,$$

and the other is

$$T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime\prime}\right)=T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)T_{r}\left(\mathbf{p}^{\prime}\rightarrow \mathbf{p}^{\prime\prime}\right).$$

We often also assume

$$\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})=\sigma_{\mathrm{t}}(\mathbf{p},-\boldsymbol{\omega}),$$

thus

$$\begin{aligned} T_{r}\left(\mathbf{p}' \rightarrow \mathbf{p}\right)&=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}'+t (-\boldsymbol{\omega}), -\boldsymbol{\omega}) dt}\\ &=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+(h-t)\boldsymbol{\omega}, \boldsymbol{\omega}) dt}\\ &=\mathrm{e}^{\int_{h}^{0} \sigma_{\mathrm{t}}(\mathrm{p}+u\boldsymbol{\omega}, \boldsymbol{\omega}) du}\\ &=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+u\boldsymbol{\omega}, \boldsymbol{\omega}) du}\\ &=T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}'\right). \end{aligned}$$

In particular, if $\sigma_{\mathrm{t}}$ is constant, we have

$$T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}h}=\mathrm{e}^{-\sigma_{\mathrm{t}}\Vert\mathbf{p} -\mathbf{p}^{\prime}\Vert}.$$

This equation is called the Beer-Lambert law.

Emission

The radiance generated per unit length in the direction $\boldsymbol{\omega}$ at point $\mathbf{p}$ in a medium is given by $L_{\mathrm{e}}(\mathbf{p}, \omega)$. This can be written as

$$\mathrm{d} L_{o}(\mathbf{p}, \omega) = L_{\mathrm{e}}(\mathbf{p}, \omega) \mathrm{d} t.$$

In-scattering

If light from other directions is scattered into the direction $\boldsymbol{\omega}$ at point $\mathbf{p}$, this scattering is called in-scattering.

We use the phase function $p(\mathbf{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o)$ to describe the distribution of scattering radiance in various directions, where $\mathbf{p}$ is the position of the point, $\boldsymbol{\omega}_i$ is the incident light direction, and $\boldsymbol{\omega}_o$ is the scattering light direction. By definition, the phase function must satisfy:

$$\int_{S^2} p(\mathbf{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) \, d\boldsymbol{\omega}_o = 1.$$

In-scattering increases the radiance in the direction $\boldsymbol{\omega}$ at point $\mathbf{p}$. Considering the radiance generated by medium emission, the total increase in radiance per unit length due to in-scattering and emission can be represented by

$$L_{\mathrm{s}}(\mathbf{p}, \boldsymbol{\omega}) = L_{\mathrm{e}}(\mathbf{p}, \boldsymbol{\omega}) + \int_{S^2} p\left(\mathbf{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right) \sigma_{\mathrm{s}}(\mathbf{p}, \boldsymbol{\omega}_i) L_{i}\left(\mathbf{p}, \boldsymbol{\omega}_i\right) \, d\boldsymbol{\omega}_i.$$

$L_{\mathrm{s}}(\mathbf{p}, \boldsymbol{\omega})$ is commonly referred to as the source term.

The Equation of Transfer

Differential-integral Equation Form

The radiance generated per unit length along the direction $\boldsymbol{\omega}$ at point $\mathbf{p}$ in the medium is given by $L_{\mathrm{e}}(\mathbf{p}, \omega)$, expressed as

$$\mathrm{d} L_{o}(\mathbf{p}, \omega)=L_{\mathrm{e}}(\mathbf{p}, \omega) \mathrm{d} t.$$

In-scattering

If at point $\mathbf{p}$, light from other directions is scattered into the direction $\boldsymbol{\omega}$, this scattering is called in-scattering.

We use the phase function $p(\mathbf{p},\boldsymbol{\omega}_i,\boldsymbol{\omega}_o)$ to describe the distribution of scattering radiance in different directions, where $\mathbf{p}$ is the position of the point, $\boldsymbol{\omega}_i$ is the incident light direction, and $\boldsymbol{\omega}_o$ is the scattered light direction. By definition, the phase function must satisfy:

$$\int_{S^2}p(\mathbf{p},\boldsymbol{\omega}_i,\boldsymbol{\omega}_o)d\boldsymbol{\omega}_o=1.$$

The in-scattering effect increases the radiance along the direction $\boldsymbol{\omega}$ at point $\mathbf{p}$. Considering the radiance generated by the medium’s emission, the total increase in radiance per unit length due to in-scattering and emission can be represented as

$$L_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega})=L_{\mathrm{e}}(\mathbf{p},\boldsymbol{\omega})+ \int_{\mathrm{S}^{2}} p\left(\mathbf{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right) \sigma_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega}_i)L_{i}\left(\mathbf{p},\boldsymbol{\omega}_i\right) d\boldsymbol{\omega}_i.$$

$L_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega})$ is usually called the source term.

The Equation of Transfer

Differential-integral Equation Form

Let $\mathbf{p}(t)=\mathbf{p}_0+t\boldsymbol{\omega}$, the rate of change of radiance in the direction $\boldsymbol{\omega}$ at point $\mathbf{p}(t)$ is determined by attenuation and the source term. The resulting equation is

$$\frac{d L_{o}(\mathbf{p}(t),\boldsymbol{\omega})}{d t}=-\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})+ L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}),$$

which is

$$\begin{aligned} &\frac{d L_{o}(\mathbf{p}(t),\boldsymbol{\omega})}{d t}\\ =\ &-\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})+L_{\mathrm{e}}(\mathbf{p}(t),\boldsymbol{\omega})+ \int_{\mathrm{S}^{2}} p\left(\mathbf{p}(t), \boldsymbol{\omega}_i, \boldsymbol{\omega}\right) \sigma_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}_i)L_{i}\left(\mathbf{p}(t),\boldsymbol{\omega}_i\right) d\boldsymbol{\omega}_i, \end{aligned}$$

and is called the equation of transfer.

Integral Equation Form

To facilitate solving, the equation of transfer can be rewritten as an integral equation in terms of $L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})$, given a boundary condition

$$L_{o}\left(\mathbf{p}(0),\boldsymbol{\omega}\right)=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right).$$

Noting that $L_{o}(\mathbf{p}(t),\boldsymbol{\omega})=L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})$, rearranging terms gives

$$\frac{d L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})}{d t}+\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})= L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}),$$

multiplying both sides by

$$e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}$$

yields

$$\begin{aligned} &\frac{d L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})}{d t}e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}+ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})\frac{d\left(e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}\right)}{dt}\\ =\ & L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}, \end{aligned}$$

which simplifies to

$$d\left(L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}\right)=L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}dt.$$

Integrating from $0$ to $t$ gives

$$\left.\left(L_{i}(\mathbf{p}(s),-\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}\right)\right|_{0}^{t}=\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds,$$

which leads to

$$L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}-L_{i}(\mathbf{p}_0,-\boldsymbol{\omega})=\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds.$$

Noting that

$$T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)=\mathrm{e}^{-\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du},$$

multiplying both sides of the equation by $T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)$ and rearranging yields

$$L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})+\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})\mathrm{e}^{-\int_{s}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds.$$

Let $t’=t-s$, i.e., $s=t-t’$, substituting yields

$$L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})-\int_{t}^0L_{\mathrm{s}}(\mathbf{p}(t-t'),\boldsymbol{\omega})\mathrm{e}^{-\int_{t-t'}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}dt'.$$

Since $\mathbf{p}(t-t’)=\mathbf{p}_0+t\boldsymbol{\omega}-t’\boldsymbol{\omega}=\mathbf{p}(t)-t’\boldsymbol{\omega}$, further simplification yields

$$L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})+\int_{0}^tT_{r}\left( \mathbf{p}(t)-t'\boldsymbol{\omega}\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}(t)-t'\boldsymbol{\omega},\boldsymbol{\omega}\right)dt'.$$

The equation

$$L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left( \mathbf{p}-t'\boldsymbol{\omega}\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}-t'\boldsymbol{\omega},\boldsymbol{\omega}\right) \mathrm{d} t'$$

is called the integral form of the transfer equation. Let $\mathbf{p}’=\mathbf{p}-t’\boldsymbol{\omega}$, the transfer equation can also be written as

$$L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left(\mathbf{p}^\prime\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right) \mathrm{d} t'$$

Figure 2 - Illustration of the Integral of Transport Equation

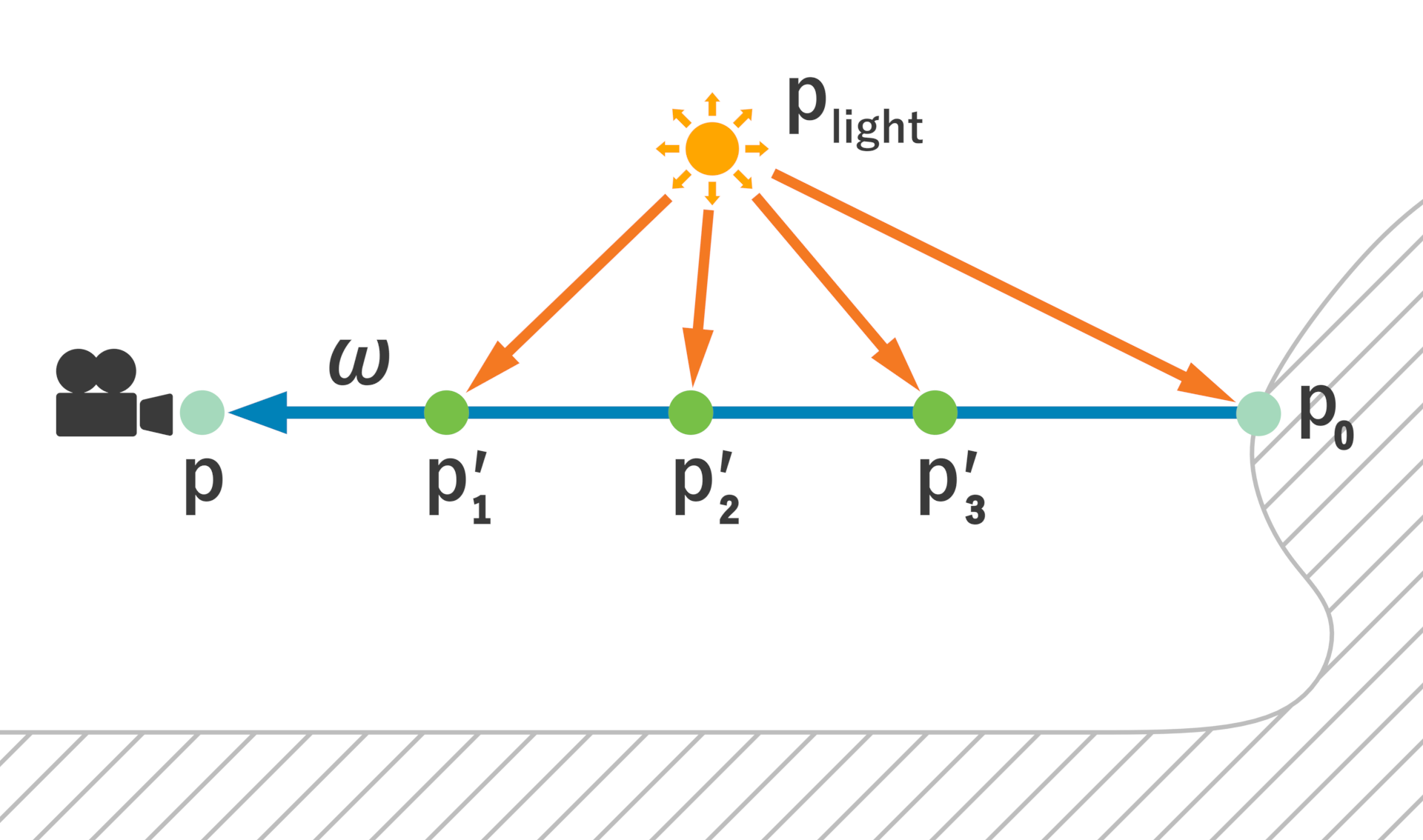
Real-time Volume Rendering

Phase Function

Assuming the phase function $p\left(\mathbf{p}^\prime, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right)$ depends only on the angle $\theta$ between $\boldsymbol{\omega}_i$ and $\boldsymbol{\omega}$, i.e.,

$$p\left(\mathbf{p}^\prime, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right)=p\left(\theta\right).$$

The simplest phase function is

$$p\left(\theta\right)=\frac{1}{4\pi}.$$

Physically-based phase functions depend on the particle size parameter $s_p$,

$$s_{p}=\frac{2 \pi r}{\lambda},$$

where $r$ is the particle radius, and $\lambda$ is the wavelength of light:

• When $s_p\ll 1$, Rayleigh scattering occurs;

• When $s_p\approx 1$, Mie scattering occurs;

• When $s_p\gg 1$, geometric scattering occurs.

Rayleigh Scattering

The phase function for Rayleigh scattering is

$$p(\theta)=\frac{3}{16 \pi}\left(1+\cos ^{2} \theta\right).$$

Figure 3 - Polar Plot of the Rayleigh Scattering Phase Function

The scattering coefficient for Rayleigh scattering is inversely proportional to the fourth power of the wavelength:

$$\sigma_{s}(\lambda) \propto \frac{1}{\lambda^{4}}.$$

Mie Scattering

The phase function for Mie scattering is given by the Henyey-Greenstein (HG) phase function:

$$p_{h g}(\theta, g)=\frac{1-g^{2}}{4 \pi\left(1+g^{2}-2 g \cos \theta\right)^{1.5}},$$

where the parameter $g\in[-1,1]$. When $g>0$, forward scattering occurs; when $g<0$, backward scattering occurs; when $g=0$, isotropic scattering occurs.

The Schlick phase function:

$$p(\theta, k)=\frac{1-k^{2}}{4 \pi(1+k \cos \theta)^{2}}, \quad \text { where } \quad k \approx 1.55 g-0.55 g^{3}$$

is an approximation of the HG phase function and is computationally faster.

Figure 4 - Polar Plots of Henyey-Greenstein (Blue) and Schlick (Red) Phase Functions with $g$ values of 0, 0.3, 0.6

Source Term Estimation

Assuming there is no emission phenomenon in the medium, the scattering coefficient only depends on the position:

$$\sigma_{\mathrm{s}}(\mathbf{p}^\prime,\boldsymbol{\omega}_i)=\sigma_{\mathrm{s}}(\mathbf{p}^\prime).$$

The source term can be approximated by:

$$\widehat{L}_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right)=\pi\sigma_{\mathrm{s}}(\mathbf{p}^\prime)\sum_{i=1}^{N_i} p\left( \theta\right)v\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right),$$

where

$$v\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\operatorname{shadowMap}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) \cdot \operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)$$

is the visibility function, where $\operatorname{shadowMap}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)$ represents the shadow map, and

$$\operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\widehat{T}_r\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)$$

represents the volume shadow. If $\sigma_t(\mathbf{p})$ is a constant $\sigma_t$, the expression for volume shadow is

$$\operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}N_j\Delta t},$$

where $N_j\Delta t$ is the distance traveled by the ray in the volume from $\mathbf{p}^\prime$ to $\mathbf{p}_{\text {light}_{i}}$.

The term $c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)$ in the source term estimation equation is the radiance of the $i$-th light, usually taken as:

$$c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)=c_{\text {light}_{i,0}}\left(\frac{r_{0}}{ \left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|}\right)^{2},$$

or

$$c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)=c_{\text {light}_{i,0}}\left(\frac{r_{0}}{\max \left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|, r_{\min }\right)}\right)^{2},$$

where $c_{\text {light}_{i,0}}$ represents the radiance of the $i$-th light when $\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|=r_0$.

Total Radiance Estimation

Assuming the attenuation coefficient $\sigma_\mathrm{t}$ only depends on position:

$$\sigma_{\mathrm{t}}(\mathbf{p}^\prime,\boldsymbol{\omega}_i)=\sigma_{\mathrm{t}}(\mathbf{p}^\prime).$$

When $\mathbf{p}_1$ and $\mathbf{p}_2$ are close, we can use

$$\widehat{T}_{r}\left(\mathbf{p}_1\rightarrow \mathbf{p}_2\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}(\mathbf{p}_1) \Delta t}$$

as an estimate for

$$T_{r}\left(\mathbf{p}_1\rightarrow \mathbf{p}_2\right)=\mathrm{e}^{-\int_{0}^{\Delta t} \sigma_{\mathrm{t}}(\mathbf{p}_1-u\boldsymbol{\omega}) du}$$

So,

$$L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left(\mathbf{p}^\prime\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right) \mathrm{d} t'$$

can be estimated as

$$\begin{aligned} \widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})&=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-S_k \Delta t} \Delta t, \end{aligned}$$

where

$$S_J=\sum\limits_{k=1}^{J}\sigma_{\mathrm{t}}(\mathbf{p}^\prime_k),\quad \mathbf{p}^\prime_k=\mathbf{p}-(k-1)\Delta t \boldsymbol{\omega} .$$

If $\sigma_t(\mathbf{p})$ is a constant $\sigma_t$, we have a more accurate estimate:

$$\begin{aligned} \widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})&=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \int_{(k-1)\Delta t}^{k\Delta t}\mathrm{e}^{-\sigma_{\mathrm{t}}t'}dt'\\ &=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\frac{1}{\sigma_{\mathrm{t}}}\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t}). \end{aligned}$$

Instance

With a constant extinction coefficient $\sigma_t$ and an isotropic phase function, the formula for calculating the radiance is given by

$$\begin{aligned} &\widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})\\ =\;&L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\frac{1}{\sigma_{\mathrm{t}}}\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t})\\ =\;&L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}\\ &+\frac{\rho(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t})}{4}\sum_{k=1}^{N_k}\mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}\sum_{i=1}^{N_i} \frac{c_{\text {light}_{i,0}}r_{0}^2}{ \left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|^2}\operatorname{shadowMap}\left(\mathbf{p}^\prime_k, \mathbf{p}_{\text {light}_{i}}\right)\mathrm{e}^{-\sigma_{\mathrm{t}}N_j\Delta t}. \end{aligned}$$