The research of color science shows that all colors perceived by human beings constitute a three-dimensional linear space. As long as a base is chosen, we can encode the color into three-dimensional coordinates and different coding methods correspond to different color spaces. This article introduces some common color spaces and how to transform one into another.

CIE RGB Color Space

Definition

Consider a discrete spectral power distribution (SPD) space, where the spectral energy is measured by radiance, the wavelength range is $380nm-720nm$, and the step length of wavelength is $0.1nm$。This space is a $3401$-dimensional linear space $\mathbb{R}^{3401}$．Under a fixed radiance, a basis is: $\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}$．

Let $C$ be the human color mapping, which maps the spectral energy distribution in SPD space to the color in the color perception space $P$. We will demonstrate that the color perception space is a 3-dimensional linear space, and the color mapping

$$C:\mathbb{R}^{3401}\longrightarrow P$$

is a linear mapping.

Firstly, since human color perception is triggered by light stimulation on the retina, $C$ must be a surjective mapping. Then, Grassmann’s law tells us that the addition in the color perception space can be well-defined as:

$$C(\mathbf{s}_1)+C(\mathbf{s}_2):=C\left(\overline{\mathbf{s}_1}+\overline{\mathbf{s}_2}\right),$$

where $\overline{\mathbf{s}_1},\overline{\mathbf{s}_2}\in\mathbb{R}^{3401}$ are any spectral energy distributions satisfying $C(\overline{\mathbf{s}_1})=C(\mathbf{s}_1)$ and $C(\overline{\mathbf{s}_2})=C(\mathbf{s}_2)$.

Furthermore, we also have a well-defined scalar multiplication: for any $k>0$ and any $\overline{\mathbf{s}}\in\mathbb{R}^{3401}$, as long as $\overline{\mathbf{s}}$ satisfies $C(\overline{\mathbf{s}})=C(\mathbf{s})$, we have

$$k\,C(s):=C(k\hspace{1pt}\overline{\mathbf{s}}).$$

Therefore, the color perception space $P$ is a linear space, and $C$ is a linear mapping. By convention, $C(\mathbf{s})$ will be abbreviated as $C\mathbf{s}$.

We can also define the subtraction in the color perception space: if there exists $\mathbf{s}_3$ such that $C\mathbf{s}_1+C\mathbf{s}_3=C\mathbf{s}_2$, then we define

$$C\mathbf{s}_2-C\mathbf{s}_1:=C\mathbf{s}_3.$$

Color matching experiments reveal the dimensionality of the color perception space. Experimental results show that red $\mathbf{v}_R=C\,\mathbf{l}_{700.0}$, green $\mathbf{v}_G=C\,\mathbf{l}_{546.1}$, and blue $\mathbf{v}_B=C\,\mathbf{l}_{435.8}$ form a basis of the color perception space. In other words, any color can be expressed as a linear combination of red, green, and blue. At the same time, any one of the colors red, green, or blue cannot be expressed as a linear combination of the other two. Therefore, the color perception space is a 3-dimensional linear space.

To avoid ambiguity, we make the following convention: the color perception space is unique, and its elements are the colors that humans can perceive. There are many color spaces, each being a set of $\mathbb{R}^3$, differing by the bijection they have with the color perception space. Simply put, facing the same point $(x_1,x_2,x_3)$, different color spaces interpret it as different colors.

If we choose the basis $\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B$ for the color perception space $P$ as mentioned earlier, then this induces a corresponding coordinate mapping

$$\mathrm{coor}_{RGB}:P\longrightarrow\mathbb{R}^3,$$

which maps colors in the color perception space $P$ to their coordinates in this basis. The $\mathbb{R}^3$ equipped with this coordinate mapping is called the CIE RGB color space.

It is easy to see that for each basis $\eta$ chosen in the color perception space $P$, the corresponding coordinate space $\mathrm{coor}_{\mathbf{\eta}}(P)$ is a color space. Since the coordinate mapping is a linear isomorphism, we call the color spaces obtained in this way linear color spaces.

Coordinate Calculation

With a basis, we can perform coordinate-based calculations, representing any color generated by an SPD with three numbers. Specifically, any SPD $\mathbf{s}\in\mathbb{R}^{3401}$ generating a color can be uniquely linearly represented by $\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B$:

$$C\mathbf{s}=R\cdot \mathbf{v}_R+G\cdot \mathbf{v}_G+B\cdot \mathbf{v}_B.$$

That is, $C\mathbf{s}$ has the coordinates $(R,G,B)$. In particular, any single-wavelength spectrum $\mathbf{l}_\lambda$ generating a color can be uniquely linearly represented by $\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B$.

$$C\,\mathbf{l}_{\lambda} =( \mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B) \begin{pmatrix} R_{\lambda} \\ G_{\lambda} \\ B_{\lambda} \end{pmatrix}.$$

Let the matrix representation of $C$ in the bases $\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}$ and $\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B$ be the color matching matrix $CMF^{RGB}$, then we have:

$$\begin{align} (C\,\mathbf{l}_{700.0},C\,\mathbf{l}_{700.1},\cdots,C\,\mathbf{l}_{720.0})&=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)\,CMF^{RGB}\\ &=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} R_{380.0} & R_{380.1}& \cdots & R_{720.0} \\ G_{380.0} & G_{380.1}& \cdots & G_{720.0} \\ B_{380.0} & B_{380.1}& \cdots & B_{720.0} \\ \end{pmatrix}. \end{align}$$

The following is the experimentally determined color matching matrix $CMF^{RGB}$ for the CIE RGB space. When the horizontal axis is $\lambda$, the vertical coordinates of the red, green, and blue curves are $R_{\lambda}, G_{\lambda}, B_{\lambda}$, respectively.

Figure 1 - CIE 1931 RGB Color Matching Function

If the color matching matrix $CMF$ is known, we can calculate the coordinates of any SPD in the CIE RGB color space. For any given SPD

$$\mathbf{s}=\left(\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}\right) \begin{pmatrix} k_{380.0} \\ k_{380.1} \\ \vdots \\ k_{720.0} \\ \end{pmatrix},$$

we have the following calculation formula:

$$C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} R_{380.0} & R_{380.1}& \cdots & R_{720.0} \\ G_{380.0} & G_{380.1}& \cdots & G_{720.0} \\ B_{380.0} & B_{380.1}& \cdots & B_{720.0} \\ \end{pmatrix} \begin{pmatrix} k_{380.0} \\ k_{380.1} \\ \vdots \\ k_{720.0} \\ \end{pmatrix}$$

Let $\mathbf{k}=(k_{380.0},k_{380.1},\cdots,k_{720.0})^T$, and partition $CMF^{RGB}$ by rows as follows:

$$CMF= \begin{pmatrix} CMF^{RGB}_1 \\ CMF^{RGB}_2 \\ CMF^{RGB}_3 \end{pmatrix},$$

The calculation formula can be rewritten as

$$C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} CMF^{RGB}_1\,\mathbf{k}\\ CMF^{RGB}_2\,\mathbf{k}\\ CMF^{RGB}_3\,\mathbf{k} \end{pmatrix}.$$

CIE rg Chromaticity Space

Any point in the color space CIE RGB can be determined by three coordinates $(R,G,B)$. The mapping is as follows:

$$\begin{align} r&=\frac{R}{R+G+B},\\ g&=\frac{G}{R+G+B},\\ b&=\frac{B}{R+G+B}=1-r-g. \end{align}$$

This reduces the three-dimensional color space CIE RGB to a two-dimensional plane. The following diagram shows the space formed by $(r,g)$, which is referred to as the CIE rg chromaticity space.

Figure 2 - CIE rg Chromaticity Space

It is not difficult to find that any straight line $t(\hat{R},\hat{G},\hat{B})$ in the CIE RGB color space, under the mapping $(R,G,B)\mapsto (r,g)$, is compressed into a point $\left(\frac{\hat{R}}{\hat{R}+\hat{G}+\hat{B}},\frac{\hat{G}}{\hat{R}+\hat{G}+\hat{B}}\right)$ in the CIE rg chromaticity space. Therefore, the chromaticity represented by $(r,g)$ is an attribute independent of irradiance. In this diagram, each point has a different chromaticity, but their irradiance can be set to the same value.

CIE XYZ Color Space

Definition

When using the color space CIE RGB derived from the basis $\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B$, some color coordinates may have negative values, which is inconvenient for calculations. Therefore, we switch to a more calculation-friendly basis $\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z$ for the color vision space, resulting in the CIE XYZ color space.

Let the transformation matrix for the basis change be $T$, we have

$$( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)=(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B)T,$$

or

$$( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)T^{-1}=(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B),$$

because

$$\begin{align} (C\,\mathbf{l}_{700.0},C\,\mathbf{l}_{700.1},\cdots,C\,\mathbf{l}_{720.0})&=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)\,CMF^{RGB}\\ &=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)T^{-1}CMF^{RGB}\\ &=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)CMF^{XYZ}, \end{align}$$

so the color matching matrix of the CIE XYZ color space $CMF^{XYZ}=T^{-1}CMF^{RGB}$. After carefully selecting $T$, the resulting $CMF^{XYZ}$ is shown in the following diagram.

Figure 3 - CIE 1931 XYZ Color Matching Function

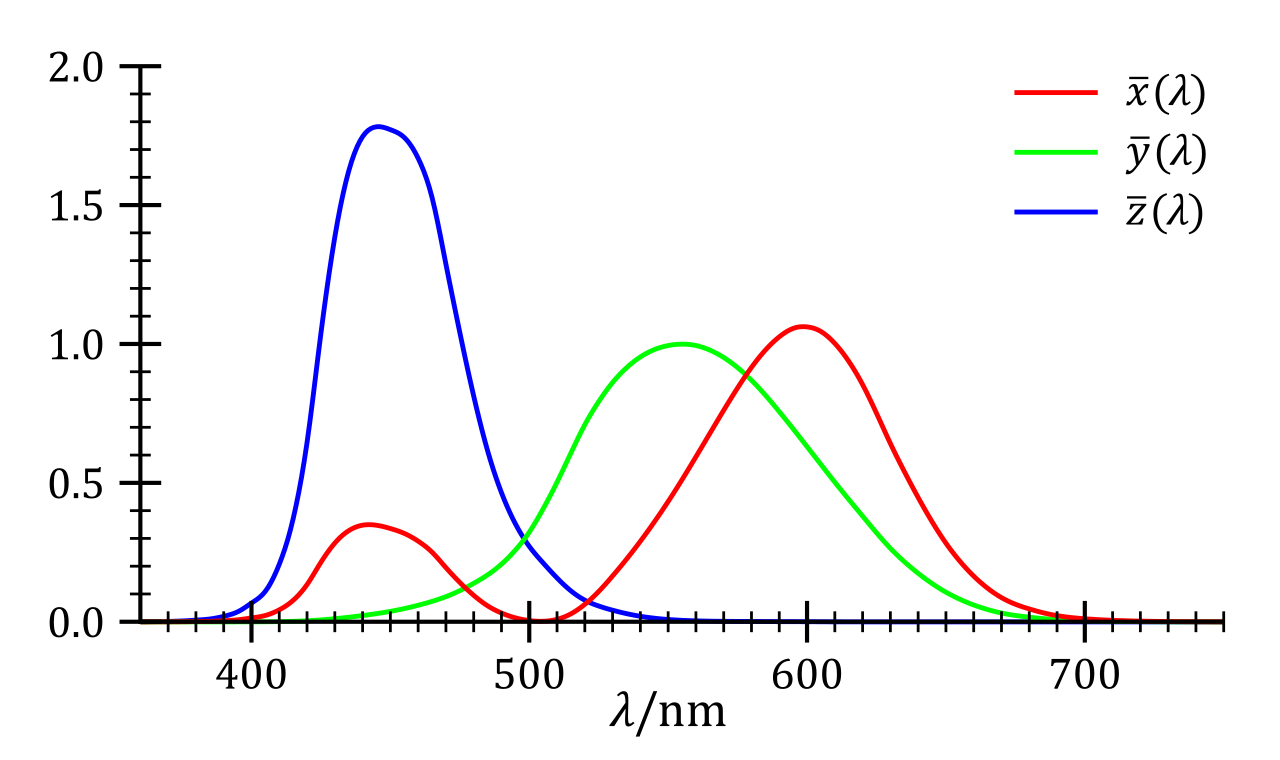
From the diagram, it can be seen that each component of the color matching matrix $CMF^{XYZ}$ is non-negative. This means that in the CIE XYZ color space, the color produced by a single frequency spectrum $C\,\mathbf{l}_{\lambda}$ always has non-negative coordinates $(X_{\lambda} , Y_{\lambda}, Z_{\lambda})$.

Representation of Luminance

Besides the non-negative coordinate components, the CIE XYZ color space also has a significant advantage in representing luminance. Luminance describes the subjective perception of the brightness of light and has the following relationship with the objective physical quantity, spectral power distribution (SPD) $SPD(\lambda)$:

$$\text{luminance}=\int_\lambda V(\lambda)SPD(\lambda)d\lambda=\sum_{i=1}^{3401}V(\lambda_i)k_{\lambda_i},\quad\lambda_i=380.0+0.1*(i-1),$$

where $\lambda$ is the wavelength, $V(\lambda)$ is the luminous efficiency function or luminosity function, and $SPD(\lambda)$ is the spectral power distribution. The diagram below shows the experimentally measured $V(\lambda)$.

Figure 4 - Luminosity Function

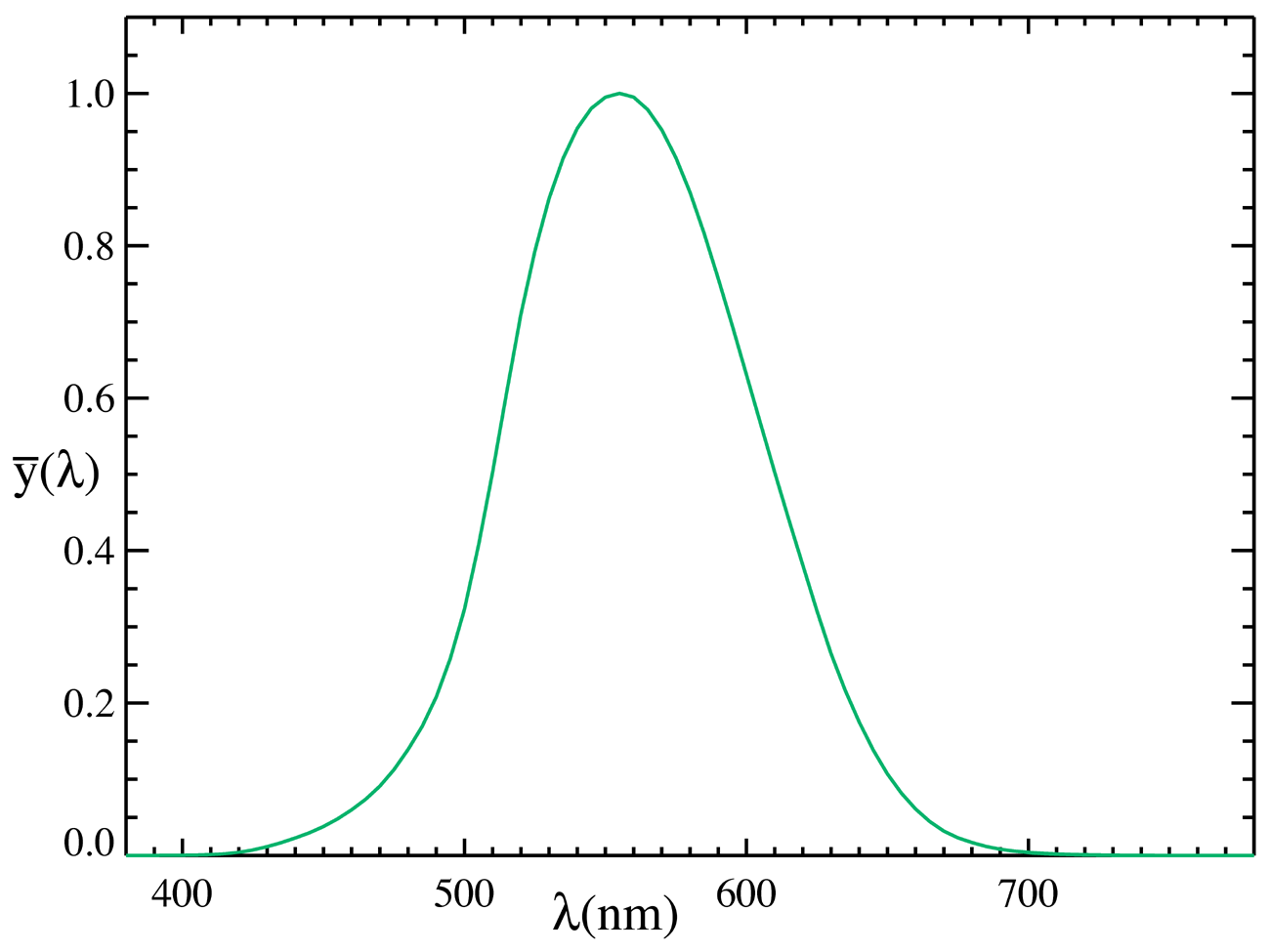
From the diagram, it can be seen that humans are most sensitive to green light. With the same irradiance, green light appears the brightest.

In fact, the $Y$ coordinate in the CIE XYZ color space can be directly used as luminance because

$$C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)CMF^{RGB}\,\mathbf{k}=(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)CMF^{XYZ}\,\mathbf{k}.$$

Let the coordinates of $C\mathbf{s}$ in the basis $(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)$ be represented as

$$C\mathbf{s}=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} X \\ Y\\ Z \end{pmatrix},$$

we have

$$\begin{pmatrix} X \\ Y \\ Z \end{pmatrix} =CMF^{XYZ}\,\mathbf{k}.$$

Let the element in the 2nd row and $j$th column of $CMF^{XYZ}$ be $Y_{\lambda_j}$, we have

$$Y=\sum_{j=1}^{3401}Y_{\lambda_j}\hspace{1pt}k_{\lambda_{j}}.$$

Since the green curve in $CMF^{XYZ}$ is very close to the $V(\lambda)$ curve, it can be approximately considered that $Y_{\lambda_j}=V(\lambda_j)$, so $Y$ can be directly used as luminance.

xyY Space and Chromaticity Diagram

By applying a nonlinear transformation to the CIE XYZ space,

$$\begin{align} x&=\frac{X}{X+Y+Z},\\ y&=\frac{Y}{X+Y+Z},\\ z&=Y, \end{align}$$

we obtain a nonlinear color space: the xyY space. Here, $x$ and $y$ represent chromaticity, and $z$ represents luminance. The following diagram is an equal-luminance chromaticity diagram, which includes all the chromaticities visible to the human eye.

Figure 5 - CIE 1931 xy Chromaticity Diagram

sRGB Color Space

Transforming from the CIE XYZ space to the sRGB space involves two steps. The first step is a basis transformation that converts the CIE XYZ space into a linear sRGB space. The second step is a Gamma transformation that converts the linear sRGB space into the final sRGB space.

Standard Illuminant

The standard illuminant CIE Standard Illuminant D65 is a relative SPD, independent of irradiance. On one hand, it forms a straight line $k(0.95047,1,1.08883)$ in the CIE XYZ space, where the point $(0.95047,1,1.08883)$ on this line with $Y=1$ is called the white point. On the other hand, it is represented as a point $(0.31271,0.32902)$ in the CIE xy chromaticity diagram.

Linear sRGB Space

Suppose the basis $(\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)$ of a color vision space $P$ derives the linear sRGB space. The basis $(\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)$ is uniquely determined by the following conditions:

1. Primaries: The CIE xy chromaticity coordinates of $\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B$ are $(0.64,0.33),(0.30,0.60),(0.15,0.06)$ respectively, i.e.,

   $$(\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)=(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} 0.64w_1&0.30w_2&0.15w_3\\ 0.33w_1&0.60w_2&0.06w_3\\ 0.03w_1&0.10w_2&0.79w_3 \end{pmatrix}.$$

2. White point: The white point $(0.95047,1,1.08883)$ in the CIE XYZ space is mapped to $(1,1,1)$ in the sRGB space, i.e.,

   $$(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} 0.95047\\ 1\\ 1.08883 \end{pmatrix} = (\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B) \begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix}.$$

By combining these two conditions, we get

$$\begin{pmatrix} 0.64&0.30&0.15\\ 0.33&0.60&0.06\\ 0.03&0.10&0.79 \end{pmatrix} \begin{pmatrix} w_1\\ w_2\\ w_3 \end{pmatrix} = \begin{pmatrix} 0.95047\\ 1\\ 1.08883 \end{pmatrix}.$$

Solving this gives

$$\begin{pmatrix} w_1\\ w_2\\ w_3 \end{pmatrix} = \begin{pmatrix} 0.644463\\ 1.19192\\ 1.20292 \end{pmatrix}.$$

Thus, the coordinate transformation formula from the CIE XYZ space to the linear sRGB space is

$$\begin{pmatrix} R_{\text {linear }} \\ G_{\text {linear }} \\ B_{\text {linear }} \end{pmatrix}=\begin{pmatrix} +3.24096994 & -1.53738318 & -0.49861076 \\ -0.96924364 & +1.8759675 & +0.04155506 \\ +0.05563008 & -0.20397696 & +1.05697151 \end{pmatrix}\begin{pmatrix} X\\ Y \\ Z \end{pmatrix}$$

Gamma Transformation

The Gamma transformation is defined as

$$\gamma(u)=\left\{\begin{array}{lll} 12.92 u & =\frac{323 u}{25} & u \leq 0.0031308 \\ 1.055 u^{1 / 2.4}-0.055 & =\frac{211 u^{\frac{5}{12}}-11}{200} & \text { otherwise } \end{array}\right.$$

This maps the coordinates in the linear sRGB space to the sRGB space, i.e.,

$$\begin{pmatrix} R_{sRGB} \\ G_{sRGB} \\ B_{sRGB} \end{pmatrix}= \begin{pmatrix} \gamma(R_{\text {linear }})\\ \gamma(G_{\text {linear }})\\ \gamma(B_{\text {linear }}) \end{pmatrix}.$$

Additionally, if any coordinate component value exceeds $1$, it will be clamped to $1$. Due to this clamping, the mapping from the CIE XYZ space to the sRGB space is not injective. Thus, the colors that can be represented by the sRGB space are a subset of those in the CIE XYZ space. The following diagram shows the chromaticity diagram of the sRGB space.

Figure 6 - CIE 1931 xy Gamut Comparison

---

Further Reading: ACES (Academy Color Encoding System)