基于图像的光照
本文最后更新于:2025年8月30日 中午
基于图像的环境光照,是指用一张图片来存储各个方向上环境光照的辐射率,并利用这张图片进行着色计算.本文介绍了基于图像的实时环境光照理论,并提供了利用Vulkan实现这一算法的源码和技术细节.
基于图像的实时环境光照
环境纹理的每一个纹素,都会存储来自某个方向的环境光的辐射率.考虑原始形式的反射方程
\[ L_o(\mathbf{p},\boldsymbol{\omega}_o)=\int_{H^2}f_{\mathrm{r}}\left(\mathbf{p}, \boldsymbol{\omega}_o, \boldsymbol{\omega}_i\right)L_i(\mathbf{p},\boldsymbol{\omega}_i)\cos\theta_i\:d\Omega_i. \]
这里我们不考虑环境光以外的其他光照,并假设环境光对于任意着色点 \(\mathbf{p}\) 都是相同的,因此环境纹理可以记作 \(L_i(\boldsymbol{\omega}_i)\).相应地,反射方程可以写作
\[ L_o(\mathbf{p},\boldsymbol{\omega}_o)=\int_{H^2}f_{\mathrm{r}}\left(\mathbf{p},\boldsymbol{\omega}_o, \boldsymbol{\omega}_i\right)L_i(\boldsymbol{\omega}_i)\cos\theta_i\:d\Omega_i. \]
在本文中,我们所需的点 \(\mathbf{p}\) 处的几何信息只有法向量 \(\mathbf{n}\),故上式可写作
\[ L_o(\mathbf{n},\boldsymbol{\omega}_o)=\int_{H^2}f_{\mathrm{r}}\left(\mathbf{n},\boldsymbol{\omega}_o, \boldsymbol{\omega}_i\right)L_i(\boldsymbol{\omega}_i)\cos\theta_i\:d\Omega_i. \]
漫反射
简化 Fresnel 项
如果只考虑漫反射,反射方程为
\[ \begin{aligned} L_o(\mathbf{n},\boldsymbol{\omega}_o)&=\int_{H^2}k_{d} f_{\text {lambert}}L_i(\boldsymbol{\omega}_i)\cos\theta_i\:d\Omega_i\\ &=\frac{\mathrm{base\_color}(1-\text {metalness})}{\pi} \int_{H^2}\left(1-F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)\right)L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) \:d\Omega_i, \end{aligned} \]
其中
\[ \begin{aligned} F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)&=F_{0}+\left(1-F_{0}\right)(1-(\mathbf{h} \cdot \boldsymbol{\omega}_o))^{5}, \\ F_{0}&=\mathrm{lerp}(0.16\:\mathrm{specular}^2, \mathrm{base\_color}, \mathrm{metalness}). \end{aligned} \]
在实时渲染中,一个常见的思路是对复杂的积分进行预计算.一般地,对任意的 \(\mathbf{n}\) 和 \(\boldsymbol{\omega}_o\),我们希望得到相应的 \(L_o(\mathbf{n},\boldsymbol{\omega}_o)\).一方面,\(\boldsymbol{\omega}_o\) 可能的取值有无穷多个.另一方面,如果考虑物体的旋转,\(\mathbf{n}\) 的取值也有无穷多个.为所有的 \(\mathbf{n}\) 和 \(\boldsymbol{\omega}_o\) 预计算出对应的 \[L_o(\mathbf{n},\boldsymbol{\omega}_o)\] 显然是不可能的.最朴素的想法是对有限个 \(\mathbf{n}\) 和 \(\boldsymbol{\omega}_o\) 进行预计算,然后对结果进行插值.但是,这要求我们制作一张 4D 的 LUT(lookup table,查找表),因而会耗费大量的空间和时间.更加经济的做法,是通过简化反射方程中需要预计算的被积函数
\[ \left(1-F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)\right)L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right), \]
让包含 \(\boldsymbol{\omega}_o\) 的被积项能够提到积分号之外.这样,我们只需为有限个 \(\mathbf{n}\) 预计算复杂的积分,并将结果存入一张 2D 的 LUT.关于 \(\boldsymbol{\omega}_o\) 的计算,则可以实时去进行.
注意到在被积函数中,只有 Fresnel 项 \(F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)\) 包含 \(\boldsymbol{\omega}_o\).因为 \(\mathbf{h}\) 包含 \(\boldsymbol{\omega}_i\),该项并不能直接提到积分之外.我们可以用简化版的 Fresnel 项 \(F^*\left(\mathbf{n},\boldsymbol{\omega}_o\right)\) 代替原本的 \(F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)\),其表达式如下
\[ \begin{aligned} F^*\left(\mathbf{n},\boldsymbol{\omega}_o\right) &=F_{0}+\left(S-F_{0}\right)\left(1-\mathbf{n}\cdot \boldsymbol{\omega}_o\right)^{5},\\ S &=\max \left\{1-\text { roughness }, F_{0}\right\}. \end{aligned} \]
于是,反射方程简化为
\[ \begin{aligned} L_o(\mathbf{n},\boldsymbol{\omega}_o) \approx\frac{\mathrm{base\_color}(1-\text {metalness})\left(1-F^*\left(\mathbf{n},\boldsymbol{\omega}_o\right)\right)}{\pi} \int_{H^2}L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) \:d\Omega_i. \end{aligned} \]
之后,我们只需为有限个 \(\mathbf{n}\) 预计算如下积分
\[ I_{\mathrm{diff}}\left(\mathbf{n}\right)=\int_{H^2}L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) \:d\Omega_i. \]
注意到该积分表示的是法线为 \(\mathbf{n}\) 的着色点接受到的环境光辐照度,因此也被称作辐照度贴图(irradiance map).
如果环境纹理是一张立方盒贴图,它的每一个纹素都会对应一个方向向量.我们可以让 \(\mathbf{n}\) 取遍所有这些方向向量,并将 \(I_{\mathrm{diff}}\left(\mathbf{n}\right)\) 的值存入对应的纹素.渲染时,\(L_o(\mathbf{n},\boldsymbol{\omega}_o)\) 由下式进行计算
\[ L^*_o(\mathbf{n},\boldsymbol{\omega}_o)=\frac{\mathrm{base\_color}(1-\text {metalness})\left(1-F^*\left(\mathbf{n},\boldsymbol{\omega}_o\right)\right)}{\pi}I_{\mathrm{diff}}\left(\mathbf{n}\right). \]
辐照度贴图的预计算
我们可以用 Monte Carlo 积分法计算
\[ I_{\mathrm{diff}}\left(\mathbf{n}\right)=\int_{H^2}L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) \:d\Omega_i. \]
我们使用 重要性采样余弦 的方法,得到 \(I_{\mathrm{diff}}\left(\mathbf{n}\right)\) 的统计量
\[ \widehat{I}_{\mathrm{diff}}\left(\mathbf{n}\right)=\frac{\pi}{N}\sum_{k=1}^NL_i(\boldsymbol{\omega}_i^{(k)}), \]
其中 \(N\) 为采样数,\(\xi_{1}^{(k)}, \xi_{2}^{(k)}\) 独立且服从均匀分布 \(U(0,1)\),
\[ \begin{align*} \boldsymbol{\omega}_i^{(k)}&=T_{\mathbf{n}} \begin{bmatrix} \sqrt{\xi_{1}} \cos \left(2 \pi \xi_{2}\right)\\ \sqrt{\xi_{1}} \sin \left(2 \pi \xi_{2}\right)\\ \sqrt{1-\xi_{1}} \end{bmatrix},\\ T_{\mathbf{n}}&=\left(\mathbf{t},\mathbf{b},\mathbf{n}\right),\\ \mathbf{u}&= \begin{cases} (0,0,1) &\mathrm{if}\; \mathbf{n}\ne(0,0,\pm1), \\ (1,0,0) & \mathrm{if}\; \mathbf{n}=(0,0,\pm1), \end{cases}\\ \mathbf{t}&=\frac{\mathbf{u}\times\mathbf{n}}{\Vert\mathbf{u}\times\mathbf{n}\Vert},\\ \mathbf{b}&=\mathbf{n}\times\mathbf{t}. \end{align*} \]
镜面反射
下面我们只考虑镜面反射,反射方程为
\[ \begin{aligned} L_o(\mathbf{n},\boldsymbol{\omega}_o)&=\int_{H^2}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)L_i(\boldsymbol{\omega}_i)\cos\theta_i\:d\Omega_i\\ &=\int_{H^2}\dfrac{F\left(\mathbf{h}, \boldsymbol{\omega}_o\right) G(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) D(\mathbf{n},\mathbf{h})}{4(\mathbf{n} \cdot \boldsymbol{\omega}_o)(\mathbf{n} \cdot \boldsymbol{\omega}_i)}L_i(\boldsymbol{\omega}_i)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) d\Omega_i. \end{aligned} \]
为化简方程,我们可以将 \(L_i(\boldsymbol{\omega}_i)\) 提出积分号外.于是,我们将 \(L_o(\mathbf{n},\boldsymbol{\omega}_o)\) 写成如下形式
\[ \begin{aligned} L_o(\mathbf{n},\boldsymbol{\omega}_o)&=\int_{S^2}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n} \cdot \boldsymbol{\omega}_i)^+ d\Omega_i \\ &=\frac{\int_{S^2}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n} \cdot \boldsymbol{\omega}_i)^+ d\Omega_i}{\int_{S^2}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)^+ d\Omega_i}\int_{S^2} f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)^+ d\Omega_i, \end{aligned} \]
希望对含 \(L_i(\boldsymbol{\omega}_i)\) 和不含 \(L_i(\boldsymbol{\omega}_i)\) 的两部分分别进行计算.
分裂和 - 第 1 部分
公式推导
直接计算
\[ \frac{\int_{H^2_{\mathbf{n}}}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n} \cdot \boldsymbol{\omega}_i) d\Omega_i}{\int_{H^2_{\mathbf{n}}}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) d\Omega_i} \]
是比较复杂的.为了降低预计算的参数空间维度.这里的假设是: lobe 的形状保持不变,始终为光线沿法线入射时的 lobe,即在计算积分时,让 \(\boldsymbol{\omega}_o, \mathbf{n}\) 的取值与 \(\boldsymbol{\omega}_o\) 的反射向量 \(\mathbf{r}(\boldsymbol{\omega}_o,\mathbf{n})=2(\boldsymbol{\omega}_o\cdot\mathbf{n})\mathbf{n}-\boldsymbol{\omega}_o\) 值相等.或者说,用 \(\mathbf{r}(\boldsymbol{\omega}_o,\mathbf{n})\) 代替被积函数中的 \(\boldsymbol{\omega}_o\) 和 \(\mathbf{n}\). 如果要用数学语言描述这种做法,可以令 \(\mathbf{n}^*=\mathbf{r}(\boldsymbol{\omega}_o,\mathbf{n})\),
\[ \begin{aligned} &\;f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)\\ =&\;f_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i, \mathbf{n}^*\right)\\ =&\;\dfrac{F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)}{4(\mathbf{n}^* \cdot \boldsymbol{\omega}_o)(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)} G(\mathbf{n}^*,\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) D(\mathbf{n}^*,\mathbf{h})\\ =&\;\dfrac{F_{0}+\left(1-F_{0}\right)(1-( \mathbf{n}^*\cdot\mathbf{h} ))^{5}}{4(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)}\frac{2(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)}{(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)(2-\alpha)+\alpha}D(\mathbf{n}^*,\mathbf{h})\\ =&\;\dfrac{F_{0}+\left(1-F_{0}\right)(1-( \mathbf{n}^*\cdot\mathbf{h} ))^{5}}{2(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)(2-\alpha)+2\alpha}D(\mathbf{n}^*,\mathbf{h}), \end{aligned} \]
其中
\[ \mathbf{h}=\frac{\boldsymbol{\omega}_i+\mathbf{n}^*}{\Vert\boldsymbol{\omega}_i+\mathbf{n}^*\Vert}. \]
用 \(f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)\) 替换 \(f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\),\(\mathbf{n}^*\) 替换 \(\mathbf{n}\),就可以得到积分的近似表达式
\[ \hspace{1.35em}\frac{\int_{H^2_{\mathbf{n}^*}}f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)^+ d\Omega_i}{\int_{H^2_{\mathbf{n}^*}}f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i\right)^+ d\Omega_i}. \]
记
\[ C(\mathbf{n}^*,\boldsymbol{\omega}_i)=\dfrac{F_{0}+\left(1-F_{0}\right)(1-( \mathbf{n}^*\cdot\mathbf{h} ))^{5}}{2(\mathbf{n}^* \cdot \boldsymbol{\omega}_i)(2-\alpha)+2\alpha}, \]
我们可以将 \[f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)\] 简写为
\[ f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)=C(\mathbf{n}^*,\boldsymbol{\omega}_i)D(\mathbf{n}^*,\mathbf{h}). \]
借助 重要性采样 GGX ,我们可以使用如下估计式
\[ \int_{H^2_{\mathbf{n}}}f(\boldsymbol{\omega}_i)D(\mathbf{h})(\mathbf{n}\cdot\boldsymbol{\omega}_i)d\Omega_i\approx\frac{4}{N}\sum_{k=1}^N\frac{\left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)\left(\mathbf{n}\cdot\boldsymbol{\omega}_i^{(k)}\right)^+}{\mathbf{n}\cdot\mathbf{h}^{(k)}}f\left(\boldsymbol{\omega}_i^{(k)}\right), \]
其中 \(\mathbf{h}^{(k)}\) 是半球 \(H^2_{\mathbf{n}}\) 上的随机变量,服从概率密度函数为
\[ pdf_{\mathbf{n}}(\mathbf{h}) =D(\mathbf{h})(\mathbf{n}\cdot\mathbf{h}) \]
的分布.因为我们假设了 \(\boldsymbol{\omega}_o=\mathbf{n}\),该估计式可以进一步化简为
\[ \int_{H^2_{\mathbf{n}}}f(\boldsymbol{\omega}_i)D(\mathbf{h})(\mathbf{n}\cdot\boldsymbol{\omega}_i)d\Omega_i\approx\frac{4}{N}\sum_{k=1}^Nf\left(\boldsymbol{\omega}_i^{(k)}\right)\left(\mathbf{n}\cdot\boldsymbol{\omega}_i^{(k)}\right)^+. \]
于是我们有
\[ \begin{aligned} &\hspace{1.35em}\hspace{1.35em}\frac{\int_{H^2_{\mathbf{n}^*}}f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n}^* \cdot \boldsymbol{\omega}_i) d\Omega_i}{\int_{H^2_{\mathbf{n}^*}}f^*_s\left(\mathbf{n}^*,\boldsymbol{\omega}_i\right)\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i\right) d\Omega_i}\\ &=\frac{\int_{H^2_{\mathbf{n}^*}}C(\mathbf{n}^*,\boldsymbol{\omega}_i)D(\mathbf{n}^*,\mathbf{h}) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n}^* \cdot \boldsymbol{\omega}_i) d\Omega_i}{\int_{H^2_{\mathbf{n}^*}}C(\mathbf{n}^*,\boldsymbol{\omega}_i)D(\mathbf{n}^*,\mathbf{h})\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i\right) d\Omega_i}\\ &\approx\frac{\sum_{k=1}^NC\left(\mathbf{n}^*,\boldsymbol{\omega}_i^{(k)}\right)L_{i}(\boldsymbol{\omega}_i^{(k)})\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+}{\sum_{k=1}^NC\left(\mathbf{n}^*,\boldsymbol{\omega}_i^{(k)}\right)\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+},\\ \end{aligned} \]
其中
\[ \mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}=2(\mathbf{n}^* \cdot\mathbf{h}^{(k)})^2-1=2\cos^2\theta_{\mathbf{h}^{(k)}}-1, \]
而 \(\mathbf{h}^{(k)}\) 是半球 \(S^2_{\mathbf{n}^*}\) 上的随机变量,服从概率密度函数为
\[ pdf(\mathbf{h})=\dfrac{\alpha^{2}\cos\theta_{\mathbf{h}}}{\pi\left(\left(\alpha^{2}-1\right)\cos^2\theta_{\mathbf{h}}+1\right)^{2}} \]
的概率分布.只要我们能够为 \(\mathbf{n}^*,\alpha,F_0\) 预计算出
\[ S(\mathbf{n}^*,\alpha,F_0)=\frac{\sum_{k=1}^NC\left(\mathbf{n}^*,\boldsymbol{\omega}_i^{(k)}\right)L_{i}(\boldsymbol{\omega}_i^{(k)})\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+}{\sum_{k=1}^NC\left(\mathbf{n}^*,\boldsymbol{\omega}_i^{(k)}\right)\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+}, \]
的值,其中
\[ C\left(\mathbf{n}^*,\boldsymbol{\omega}_i^{(k)}\right)=\dfrac{F_{0}+\left(1-F_{0}\right)(1-( \mathbf{n}^*\cdot\mathbf{h}^{(k)} ))^{5}}{2(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)})(2-\alpha)+2\alpha}, \]
那么在渲染时,对任意的 \(\boldsymbol{\omega}_o\), \(\mathbf{n}\), \(\alpha\) 和 \(F_0\),第一部分分裂积分可估计为
\[ \frac{\int_{H^2_{\mathbf{n}}}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) L_{i}(\boldsymbol{\omega}_i)(\mathbf{n} \cdot \boldsymbol{\omega}_i) d\Omega_i}{\int_{H^2_{\mathbf{n}}}f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) d\Omega_i}\approx S(\mathbf{r}(\boldsymbol{\omega}_o,\mathbf{n}),\alpha,F_0). \]
值得一提的是,虚幻引擎在实验中发现:即使在得到的估计式去掉 \(C(\mathbf{n}^*,\boldsymbol{\omega}_i)\),仅使用
\[ \frac{\sum_{k=1}^NL_{i}(\boldsymbol{\omega}_i^{(k)})\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+}{\sum_{k=1}^N\left(\mathbf{n}^* \cdot \boldsymbol{\omega}_i^{(k)}\right)^+}, \]
进行估计,效果也不错.同时,这也会让预计算和实时计算更加简单.本文则尝试保留 \(C(\mathbf{n}^*,\boldsymbol{\omega}_i)\),目的在于展示另一种可能的做法.
预计算
为了简化对 \(S(\mathbf{n}^*,\alpha,F_0)\) 的预计算,我们只计算 \(F_0\) 为 \(0\) 和 \(1\) 的情况.确定 \(F_0\) 后每给定一个 \(\alpha\),我们就可以让 \(\mathbf{n}^*\) 取各个方向,预计算出
\[S(\mathbf{n}^*,\alpha,F_0)\]
的值,得到一张立方盒贴图.因为当 \(\alpha\) 较小时,变动 \(\alpha\) 产生的视觉效果改变更加剧烈,我们令 \(\text{roughness}=\sqrt{\alpha}\),转而去预计算
\[S(\mathbf{n}^*,\text{roughness},F_0).\]
对不同的 \(\text{roughness}\),我们可以像 Mipmap 一样生成多张立方盒贴图.\(\text{roughness}\) 越大,生成的立方盒贴图分辨率就越小.对于其它的 \(\text{roughness}\),\(S(\mathbf{n}^*,\text{roughness},F_0)\) 的值可由 Mipmap 进行三线性插值得到.而对于 \(F_0\) 不为 \(0\) 和 \(1\) 的情况,则对结果再进行一次线性插值.这些预计算得到的立方盒贴图,被称作 预过滤环境贴图(pre-filtered environment map).
在计算 \(S(\mathbf{n}^*,\text{roughness},F_0)\) 时,我们既可以选择采样 \(\mathbf{h}^{(k)}\),也可以选择采样 \(\boldsymbol{\omega}_i^{(k)}\),视具体情况而定。比如说,当 \(F_0=1\) 时含 \(\mathbf{h}^{(k)}\) 的项会消失,这时我们可以选择采样 \(\boldsymbol{\omega}_i^{(k)}\).
设 \(\xi_{1}^{(k)}, \xi_{2}^{(k)}\) 独立且服从均匀分布 \(U(0,1)\),\(T_{\mathbf{n}}\) 与之前的定义相同,\(\boldsymbol{\omega}_i^{(k)}\) 的采样方案为
\[ \boldsymbol{\omega}_i^{(k)}=T_{\mathbf{n}} \begin{bmatrix} \dfrac{2\alpha\cos2\pi\xi_{2}^{(k)}\sqrt{\xi_{1}^{(k)}\left(1-\xi_{1}^{(k)}\right)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}\\ \\ \dfrac{2\alpha\sin2\pi\xi_{2}^{(k)}\sqrt{\xi_{1}^{(k)}\left(1-\xi_{1}^{(k)}\right)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}\\ \\ \dfrac{1-(1+\alpha^2)\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}} \end{bmatrix}. \]
该采样方案是利用特殊关系
\[ \cos\theta_{i}^{(k)}=2\cos^2\theta_{\mathbf{h}^{(k)}}-1, \]
先从 \(\mathbf{h}^{(k)}\) 的切空间球坐标
\[ \begin{aligned} \theta_{\mathbf{h}^{(k)}}&=\arccos\sqrt{\frac{1-\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}},\\ \varphi_{\mathbf{h}^{(k)}}&=2\pi\xi_{2}^{(k)}, \end{aligned} \]
导出 \(\boldsymbol{\omega}_i^{(k)}\) 的切空间球坐标
\[ \begin{aligned} \theta_{i}^{(k)}&=\arccos\frac{1-(1+\alpha^2)\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}},\\ \varphi_{i}^{(k)}&=2\pi\xi_{2}^{(k)}, \end{aligned} \]
然后再转化为直角坐标系得到.
分裂和 - 第 2 部分
公式推导
分裂积分的右边可以化简为
\[ \begin{aligned} &\; \int_{H^2_{\mathbf{n}}} f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) d\Omega_i\\ =&\;\int_{H^2_{\mathbf{n}}}\left(F_{0}+\left(1-F_{0}\right)(1-( \mathbf{h} \cdot \boldsymbol{\omega}_o ))^{5}\right) \frac{f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)}{F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)}\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)d\Omega_i\\ =&\; F_{0}\int_{H^2_{\mathbf{n}}} \frac{f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)}{F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)} \left(1-(1-( \mathbf{h} \cdot \boldsymbol{\omega}_o ))^{5}\right)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)d\Omega_i\\&+\int_{H^2_{\mathbf{n}}} \frac{f_s(\mathbf{n},\boldsymbol{\omega}_i, \boldsymbol{\omega}_o)}{F\left(\mathbf{h}, \boldsymbol{\omega}_o\right)}(1-( \mathbf{h} \cdot \boldsymbol{\omega}_o ))^{5}\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) d\Omega_i\\ =&\; F_{0}\int_{H^2_{\mathbf{n}}} \dfrac{ G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) D(\mathbf{h})}{4(\mathbf{n} \cdot \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)} \left(1-(1-( \mathbf{h} \cdot \boldsymbol{\omega}_o ))^{5}\right)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)\,d\Omega_i\\&+\int_{H^2_{\mathbf{n}}} \dfrac{ G(\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) D(\mathbf{h})}{4(\mathbf{n} \cdot \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right)}(1-( \mathbf{h} \cdot \boldsymbol{\omega}_o ))^{5}\left(\mathbf{n} \cdot \boldsymbol{\omega}_i\right) \,d\Omega_i\\ =&AF_0+B. \end{aligned} \]
再次使用 重要性采样 GGX 的估计式
\[ \int_{H^2_{\mathbf{n}}}f(\boldsymbol{\omega}_i)D(\mathbf{h})(\mathbf{n}\cdot\boldsymbol{\omega}_i)d\Omega_i\approx\frac{4}{N}\sum_{k=1}^N\frac{\left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)\left(\mathbf{n}\cdot\boldsymbol{\omega}_i^{(k)}\right)^+}{\mathbf{n}\cdot\mathbf{h}^{(k)}}f\left(\boldsymbol{\omega}_i^{(k)}\right) \]
我们可以得到
\[ \begin{aligned} A &\approx \frac{4}{N}\sum_{k=1}^N\frac{\left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)\left(\mathbf{n}\cdot\boldsymbol{\omega}_i^{(k)}\right)^+}{\mathbf{n}\cdot\mathbf{h}^{(k)}}\dfrac{ G(\boldsymbol{\omega}_i^{(k)}, \boldsymbol{\omega}_o) }{4(\mathbf{n} \cdot \boldsymbol{\omega}_o)\left(\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}\right)}\left(1-(1-( \mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o ))^{5}\right)\\ &=\frac{1}{N} \sum_{k=1}^{N} \dfrac{ G(\boldsymbol{\omega}_i^{(k)}, \boldsymbol{\omega}_o) \left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)}{(\mathbf{n} \cdot \boldsymbol{\omega}_o)\left(\mathbf{n}\cdot\mathbf{h}^{(k)}\right)} \left(1-(1-( \mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o ))^{5}\right)\mathbb{1}_{\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}>0},\\ &=\frac{1}{N} \sum_{k=1}^{N} \dfrac{ 2\left(\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}\right)^+ \left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)}{\left(\Lambda(\boldsymbol{\omega}_o)+\Lambda\left(\boldsymbol{\omega}_i^{(k)}\right)\right)\left(\mathbf{n}\cdot\mathbf{h}^{(k)}\right)} \left(1-(1-( \mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o ))^{5}\right), \end{aligned} \]
\[ B \approx \frac{1}{N} \sum_{k=1}^{N} \dfrac{ 2\left(\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}\right)^+ \left(\mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o\right)}{\left(\Lambda(\boldsymbol{\omega}_o)+\Lambda\left(\boldsymbol{\omega}_i^{(k)}\right)\right)\left(\mathbf{n}\cdot\mathbf{h}^{(k)}\right)} \left(1-( \mathbf{h}^{(k)} \cdot \boldsymbol{\omega}_o )\right)^{5}, \]
其中
\[ \begin{aligned} \boldsymbol{\omega}_i^{(k)}&=\mathbf{r}(\boldsymbol{\omega}_o,\mathbf{h}^{(k)})=2(\boldsymbol{\omega}_o\cdot\mathbf{h}^{(k)})\mathbf{h}^{(k)}-\boldsymbol{\omega}_o,\\ \Lambda\left(\boldsymbol{\omega}_o\right)&=\left(\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}\right)((\mathbf{n} \cdot \boldsymbol{\omega}_o)(1-\alpha)+\alpha), \\ \Lambda\left(\boldsymbol{\omega}_i^{(k)}\right)&=\left(\mathbf{n} \cdot \boldsymbol{\omega}_o\right)\left(\left(\mathbf{n} \cdot \boldsymbol{\omega}_i^{(k)}\right)(1-\alpha)+\alpha\right) . \end{aligned} \]
预计算
因为 BRDF 是各向同性的,计算结果仅依赖于 \(\mathbf{n} \cdot \boldsymbol{\omega}_o\) 和 \(\alpha\) 的取值.于是,给定 \(\mathbf{n} \cdot \boldsymbol{\omega}_o=c\), 我们可以取特殊的 \(\mathbf{n}\) 和 \(\boldsymbol{\omega}_o\) 进行计算.例如说,取 \(\mathbf{n}=(0,0,1)\), \(\boldsymbol{\omega}_o=\left(\sqrt{1-c^2},0,c\right)\) . 以 \(\mathbf{n} \cdot \boldsymbol{\omega}_o\) 为横轴,\(\alpha\) 为纵轴,可以计算出一张 2D LUT,它的 R、G 通道分别表示 A、B 的值.
根据我们在 重要性采样 GGX 这一节得到的结果,设 \(\xi_{1}^{(k)}, \xi_{2}^{(k)}\) 独立且服从均匀分布 \(U(0,1)\),\(\mathbf{h}^{(k)}\) 的采样方案为
\[ \mathbf{h}^{(k)}=\begin{bmatrix} \alpha\cos2\pi\xi_{2}^{(k)}\sqrt{\dfrac{\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}}\;\\ \\ \alpha\sin2\pi\xi_{2}^{(k)}\sqrt{\dfrac{\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}}\\ \\ \sqrt{\dfrac{1-\xi_{1}^{(k)}}{1-(1-\alpha^2)\xi_{1}^{(k)}}}\end{bmatrix}. \]
基于Vulkan的算法实现
环境纹理
矩形环境纹理
在 Poly Haven 网站上,我们可以免费下载 CC0 授权的高动态范围(HDR)环境纹理.该网站提供的这些环境纹理都是通过如下 等距矩形投影 得到的
\[ \begin{aligned} u&=\frac{1}{2\pi}\varphi=\frac{1}{2\pi}\mathrm{mod}\left(\mathrm{arctan2}\left(\frac{y}{x}\right),2\pi\right),\\ v&=\frac{1}{\pi}\theta=\frac{1}{\pi}\arccos \frac{z}{r}, \end{aligned} \]
其中 \((x,y,z)\) 和 \((r,\theta,\varphi)\) 分别是方向向量的直角坐标与球坐标,\((u,v)\) 是归一化到 \([0,1]\) 区间的纹理坐标,函数 \(\mathrm{arctan2}\) 的定义为
\[ \operatorname{arctan2}(y, x)= \begin{cases}\arctan \left(\frac{y}{x}\right) & \text { if } x>0, \\ \arctan \left(\frac{y}{x}\right)+\pi & \text { if } x<0 \text { and } y \geq 0, \\ \arctan \left(\frac{y}{x}\right)-\pi & \text { if } x<0 \text { and } y<0, \\ +\frac{\pi}{2} & \text { if } x=0 \text { and } y>0, \\ -\frac{\pi}{2} & \text { if } x=0 \text { and } y<0, \\ \text { undefined } & \text { if } x=0 \text { and } y=0,\end{cases} \]
图像为

取模函数 \(\mathrm{mod}\) 的定义为
\[ \mathrm{mod}(x,m) = x-m\left\lfloor\frac{x}{m}\right\rfloor. \]
实际中,纹理的宽度与高度之比通常为 \(2:1\).下图就是一张通过等距矩形投影(equirectangular projection)得到的环境纹理.

存储辐射率的所有方向构成了一个球面,我们暂且称之为环境光球面.需要指出的是,一些 3D 软件在解释环境纹理时,会认为环境纹理是贴在环境光球面内部的.以上图为例,如果在 Blender 软件中打开这张环境纹理,我们会发现蓝色的牌子在白色的牌子左边.
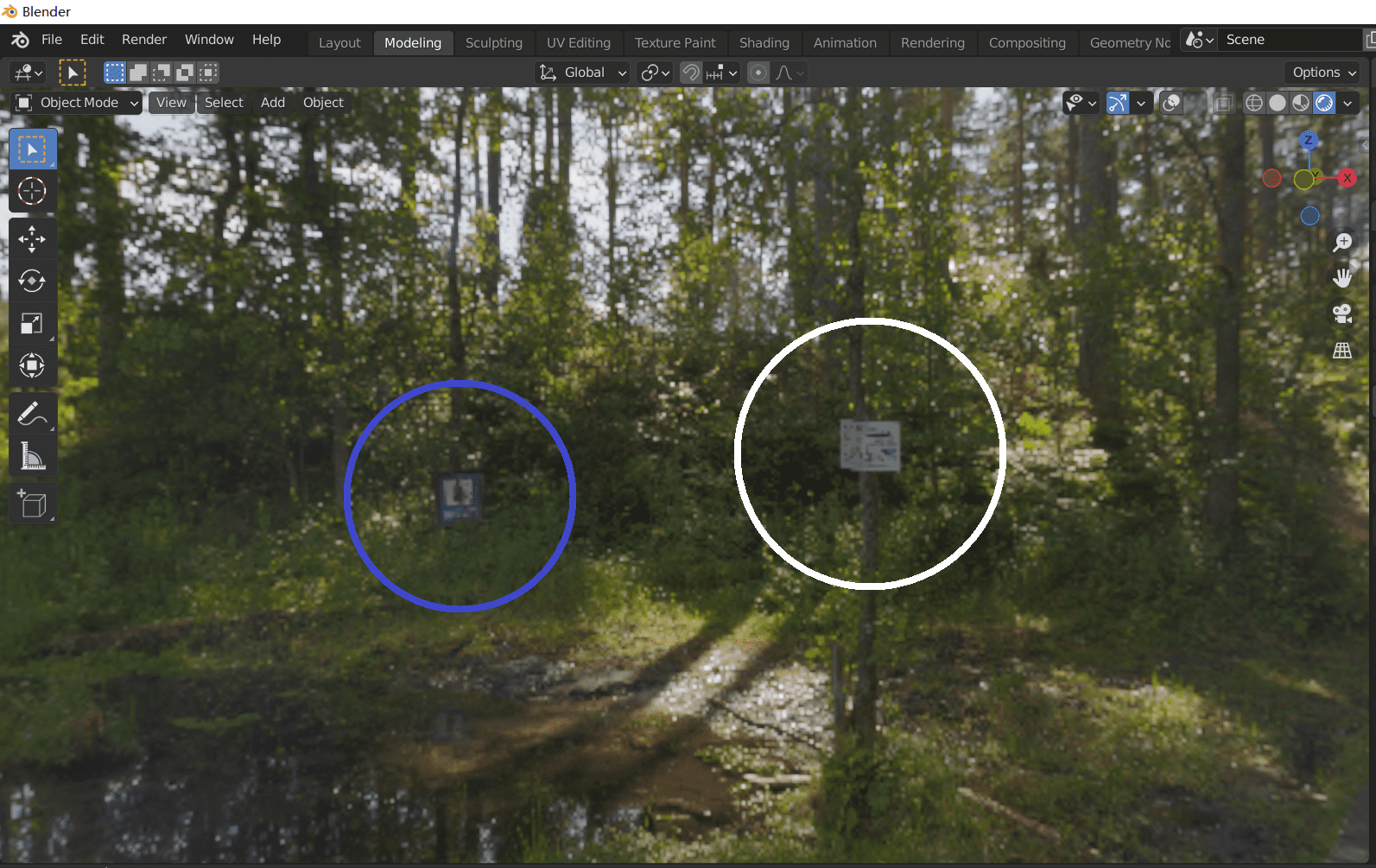
观察原始的矩形环境纹理,蓝色牌子同样在白色牌子左边.这就说明,Blender 在解释环境纹理时,使用的等距矩形投影其实是下式
\[ \begin{aligned} \tilde{u}&=1-u=1-\frac{1}{2\pi}\varphi,\\ \tilde{v}&=v=\frac{1}{\pi}\theta. \end{aligned} \]
立方盒贴图
除了这种矩形环境纹理,立方盒贴图(Cubemap)也常常被用作环境纹理.存储辐射率的所有方向构成了一个球面,立方盒贴图可以看作是把球面上每一点,沿径向投影到与球面中心重合的立方体的表面上.因此,立方盒贴图是由立方体 6 个表面的 6 张正方形贴图共同组成的.因为相对于矩形环境纹理而言,采样立方盒贴图在性能上更有优势,我们在 Vulkan 中也将使用这种立方盒贴图作为环境纹理.
在继续介绍立方盒贴图之前,我们要先讲清楚 Vulkan 的坐标系问题.OpenGL 使用如下世界坐标系
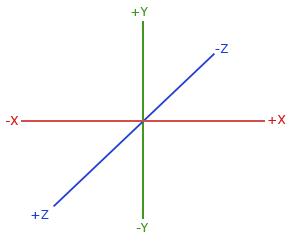
Vulkan 使用的世界坐标系则与 OpenGL 不同.但为了使用基于 OpenGL
坐标系的数学库 GLM,我对
VkViewport 对象进行了如下设置. 1
2
3
4
5VkViewport viewport{};
viewport.width = renderer.extent.width;
viewport.height = -renderer.extent.height;
viewport.x = 0;
viewport.y = renderer.extent.height;
接下来,我们介绍 Vulkan 对于立方盒贴图的规定.首先,与矩形环境纹理贴在环境光球面内部不同,6 张立方盒贴图是贴在立方盒外部的. 下图是图 1 对应的立方盒贴图.

放大观察,会发现此时蓝色牌子跑到了白色牌子的右边(见图6左).但如果我们对立方盒贴图进行采样,然后将它当作环境光进行渲染,得到的显示结果是蓝色牌子在白色牌子的左边(见图6右).这就表明,立方盒贴图确实是贴在立方盒外部的.(立方盒贴图渲染程序的源码见 003_Vulkan_Skybox,具体实现的细节会在之后进行介绍)

事实上,Vulkan 对立方盒贴图布局的规定可以由下图表明.

以 FACE 0 为例,\(+X\) 表示该图贴在 \(+X\) 轴所指的立方体的面上,也即立方体的右面.左下角的坐标轴 \((-z,y)\),标明了这张贴图在世界空间的朝向:向右是 \(-z\) 方向,向上是 \(y\) 方向.右上角的坐标轴 \((u,v)\) 则标明了这张贴图在纹理空间的朝向.这也印证了我们之前所说的:立方盒贴图是贴在立方体外部的.
在 Vulkan 中,立方盒贴图的 6 张图对应 VkImage 对象的 6
层.需要注意的是,6 张图片的顺序必须与图 6 所示的 FACE 0 到 FACE 5
的顺序一致.
从磁盘读写环境纹理
因为环境纹理存储的是辐射率,所以一般情况下图片格式均为浮点类型.最常见的图片格式是 HDR 和 EXR.
HDR 图片的每个纹素占用 32 比特,采用 R8G8B8E8
的编码方式,即每个色彩通道是 8 比特,三个色彩通道共用 8
比特的指数.我们使用只含头文件的轻量级开源库 stb 对它进行读写.读 HDR
可以使用 stbi_loadf 函数,返回的指针所指内存的布局为
R32G32B32A32 ,即 4 通道浮点格式.写 HDR 可以使用
stbi_write_hdr 函数,将布局为 R32G32B32A32 的数据存为
HDR.
EXR 图片的格式比较复杂.对于环境纹理而言,最常用的是 B32G32R32 布局的
3 通道浮点格式,和 B16G16R16 布局的 3
通道半精度浮点格式.我们使用只含头文件的轻量级开源库 tinyexr 对它进行读写.读 EXR
可以使用 LoadEXR 函数,对于
B32G32R32、B16G16R16、A32B32G32R32、A16B16G16R16 格式的 EXR
图片,返回的指针所指内存的布局均为 R32G32B32A32 ,即 4 通道浮点格式.写
EXR 可以用 SaveEXRImageToFile 函数,将布局为 R32G32B32A32
的数据存为指定格式的 EXR 图片.
矩形纹理转立方盒贴图
完整程序源码见EquirectangularTo Cubemap.
将矩形纹理转成立方盒贴图,思路就是把矩形纹理贴到一个立方体上,然后分别对立方体的 6 个面进行拍屏,使立方体的表面正好占据整个屏幕空间.
下面的代码会输出投影矩阵和观察矩阵的乘积,分别表示从右、左、上、下、前、后架设摄像机拍摄立方体.
1
2
3
4
5
6
7
8
9
10
11
12
13
14glm::mat4 captureProjection =
glm::perspective((float)M_PI / 2.0f, 1.0f, 0.1f, 10.0f);
glm::mat4 captureViews[] = {
glm::lookAt(glm::vec3(2.0f, 0.0f, 0.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f)),
glm::lookAt(glm::vec3(-2.0f, 0.0f, 0.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f)),
glm::lookAt(glm::vec3(0.0f, 2.0f, 0.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 0.0f, -1.0f)),
glm::lookAt(glm::vec3(0.0f, -2.0f, 0.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 0.0f, 1.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, 2.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f)),
glm::lookAt(glm::vec3(0.0f, 0.0f, -2.0f), glm::vec3(0.0f, 0.0f, 0.0f), glm::vec3(0.0f, 1.0f, 0.0f))
};
for (int i = 0; i < 6; i++)
{
std::cout << glm::to_string(captureProjection * captureViews[i]) << std::endl;
}
我们可以将输出的矩阵复制到顶点着色器中进行着色.下面是顶点着色器的代码.
1 | |
这里我们不打算依靠 UV 映射为立方体去贴纹理,而是根据世界坐标去贴纹理,所以需要将世界坐标传入片元着色器.片元着色器的代码如下.
1 | |
片元着色器中,SampleSphericalMap
函数基本上就是之前提到的投影 \[
\begin{aligned}
\tilde{u}&=1-\frac{1}{2\pi}\mathrm{mod}\left(\mathrm{arctan2}\left(\frac{y}{x}\right),2\pi\right),\\
\tilde{v}&=\frac{1}{\pi}\arccos \frac{z}{r}.
\end{aligned}
\]
但是,具体形式上有所差别.一是因为如果不在意贴图是否发生了旋转,那么取模函数
\(x\mapsto\mathrm{mod}(x,2\pi)\)
可以用平移函数 \(x\mapsto x+\pi\)
进行替换.二是因为我们在 Vulkan
中使用的坐标系与本文在数学推导时采用的坐标系不同,在将本文公式转化为
GLSL 代码时,应该先把公式中所有的向量 \(\mathbf{v}=(x,y,z)\) 用 \(\mathbf{v}'=(y,z,x)\)
进行替换.例如,公式中出现的所有向量 \((0,0,1)\),都应该用 \((0,1,0)\) 进行替换.
Vulkan中的立方盒贴图
在 Vulkan 中,在为立方盒贴图创建 VkImage
对象时,需要如下创建信息. 1
2
3
4VkImageCreateInfo imageInfo{};
//...
imageInfo.arrayLayers = 6;
imageInfo.flags = VK_IMAGE_CREATE_CUBE_COMPATIBLE_BIT;
其他涉及到VkImage的操作,也同样要将图片的层数layerCount设置为
6.比如说,如果使用了 staging
buffer,在进行vkCmdCopyBufferToImage时,要设置
1 | |
在使用vkCmdPipelineBarrier时,要设置
1 | |
在使用vkCmdBlitImage创建 Mipmap 的时候,也要设置
1 | |
在为立方盒贴图创建 VkImageView
对象时,需要如下创建信息. 1
2
3
4VkImageViewCreateInfo viewInfo{};
//...
viewInfo.viewType = VK_IMAGE_VIEW_TYPE_CUBE;
viewInfo.subresourceRange.layerCount = 6;
立方盒贴图的渲染
完整程序源码见VulkanSkybox.
在渲染立方盒贴图时,我们要消除摄像机观察矩阵中的平移,因此会对观察矩阵做如下处理.
1 | |
着色器的代码就是简单地渲染一个立方体.只需要注意,在采样立方盒贴图时,需要使用一个一个vec3类型的方向向量作为纹理坐标.
1 | |
1 | |
预计算
辐照度贴图
完整程序源码见IrradianceMap.
1 | |

预过滤环境贴图
完整程序源码见Pre-filteredMap.
1 | |
我们选取 \(\text{roughness}=0.0, 0.2, 0.4, 0.6, 0.8, 1.0\) 这 6 个值进行预计算.当 \(F_0=1\) 时,\(2^{19}=524288\) 次采样下得到的预过滤贴图如下.

BRDF 二维查找表
完整程序源码见BRDF2D LUT.
1 | |
采样数为 65536 时,得到的结果如下.
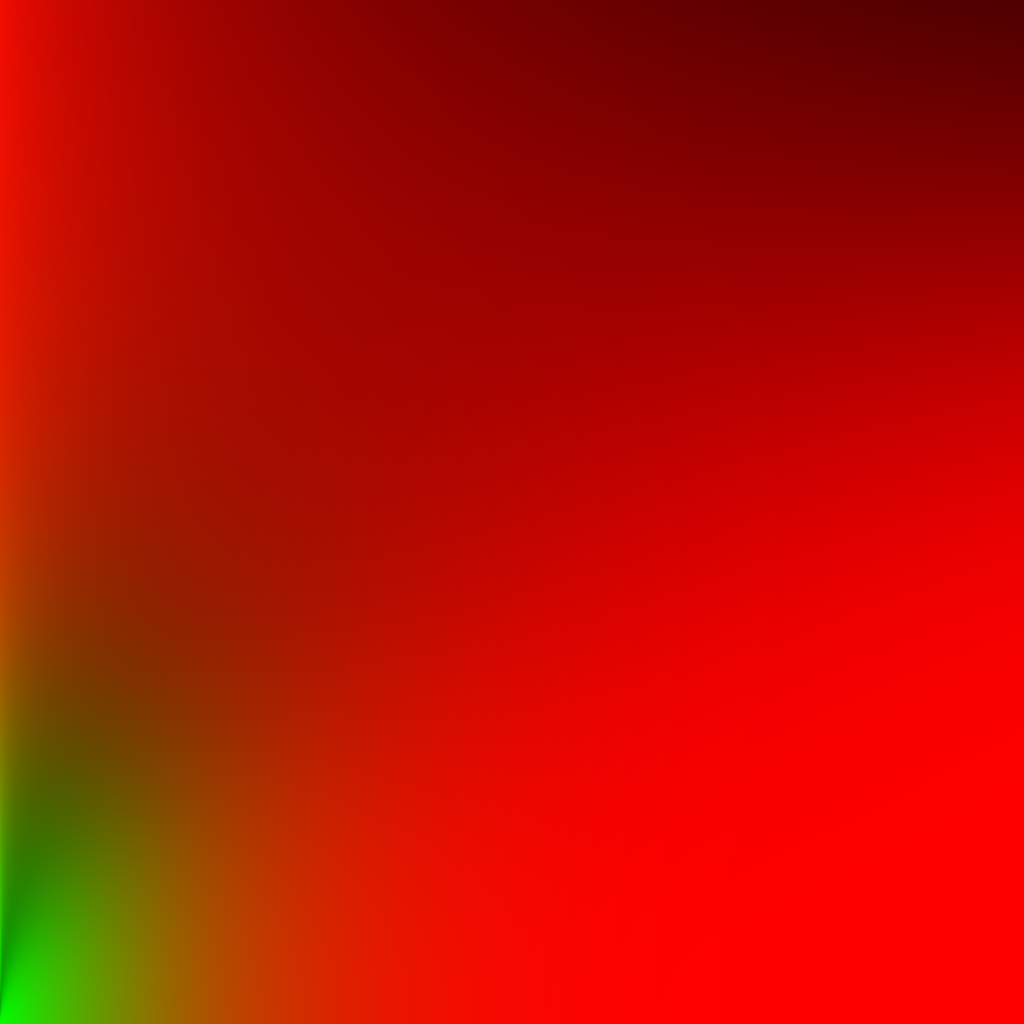
实时渲染
完整程序源码见ImageBased Lighting.
1 | |
本博客所有文章除特别声明外,均采用 CC BY-SA 4.0 协议 ,转载请注明出处!