体积渲染不仅要考虑光线与物体表面的交互，还要考虑与空间中大量微粒的交互。本文介绍了体积渲染的一般理论，导出了积分方程形式的光线传输方程，最后给出了实时体积渲染的实例。

体积介质

体积介质（media）由体积内部的大量微粒构成．光在介质中传播时，可能会出现 3 种情况：透过（transmission）、吸收（absorption）、散射（scattering）．

图1 - 光线与微粒的作用

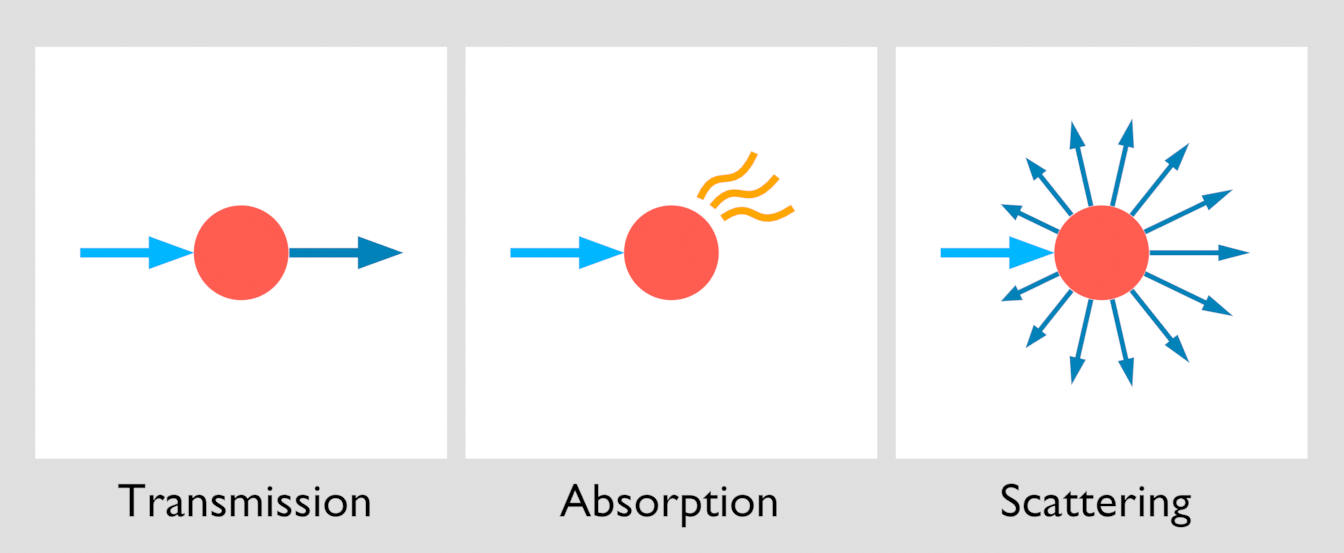
同时，介质本身还可能存在发射（emission）的现象．

吸收

吸收是由介质的 吸收截面（absorption cross section）所描述的，通常记作 \(\sigma_a\)．假设沿 \(\boldsymbol{\omega}\) 方向的光线与点 \(\bf p\) 处的介质发生作用，\(\sigma_a(\mathbf{p},\boldsymbol{\omega})\) 表示光线在点 \(\bf p\) 处沿 \(\boldsymbol{\omega}\) 方向行进单位长度后，被吸收的辐射率占原先辐射率的比值，也可以理解为光被吸收的概率．如果不考虑光在介质中的散射，即光始终沿直线传播，那么我们可以得到关于辐射率的如下公式

\[ d L_{o}(\mathbf{p},\boldsymbol{\omega})=-\sigma_{a}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}) d t. \]

外散射

如果沿 \(\boldsymbol{\omega}\) 方向行进的光线，在点 \(\bf p\) 处被散射到了其他方向，那么我们称此时的散射为 外散射（out-scattering）．散射系数（scattering coefficient）\(\sigma_s(\mathbf{p},\boldsymbol{\omega})\) 表示光在点 \(\bf p\) 处沿 \(\boldsymbol{\omega}\) 方向行进单位长度后，被外散射的辐射率占原先辐射率的比值．外散射现象与吸收现象类似，都会导致点 \(\bf p\) 处沿 \(\boldsymbol{\omega}\) 方向出射的辐射率 \(L_{o}(\mathbf{p},\boldsymbol{\omega})\) 减小．外散射导致的辐射率变化率可由下式描述

\[ \frac{d L_{o}(\mathbf{p},\boldsymbol{\omega})}{d t}=-\sigma_{s}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}) . \]

吸收和外散射的合效应称为 衰减（attenuation）或者 灭减（extinction）．衰减系数 \(\sigma_{t}\) 定义为

\[ \sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})=\sigma_{a}(\mathbf{p},\boldsymbol{\omega})+\sigma_{s}(\mathbf{p},\boldsymbol{\omega}). \]

衰减效应可由下式描述

\[ \frac{d L_{o}(\mathbf{p},\boldsymbol{\omega})}{d t}=-\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega}) L_{i}(\mathbf{p},-\boldsymbol{\omega}). \]

有两个与衰减系数相关的量也很常见．一个是 反射率（albedo）\(\rho\)，由下式定义

\[ \rho=\frac{\sigma_{s}}{\sigma_{\mathrm{t}}}=\frac{\sigma_{s}}{\sigma_a+\sigma_{s}}. \]

表示外散射效应占衰减效应的比重．另一个是 平均自由程（mean free path）\(1/\sigma_t\)，表示一个光子沿直线行进而不被吸收或散射的平均距离．

如果只考虑衰减效应，则有 \(L_{o}(\mathbf{p},\boldsymbol{\omega})=L_{i}(\mathbf{p},-\boldsymbol{\omega})\)，从而有

\[ d \ln L_{o}(\mathbf{p},\boldsymbol{\omega})=-\sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})dt. \]

设 \(\mathbf{p}'=\mathbf{p}+h\boldsymbol{\omega}\)，从 \(\mathbf{p}\) 到 \(\mathbf{p}'\) 点积分可得

\[ \ln L_{o}(\mathbf{p}',\boldsymbol{\omega})-\ln L_{o}(\mathbf{p},\boldsymbol{\omega})=-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+t \boldsymbol{\omega}, \boldsymbol{\omega}) dt, \]

即

\[ T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)=\frac{L_{o}(\mathbf{p}',\boldsymbol{\omega})}{L_{o}(\mathbf{p},\boldsymbol{\omega})}=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+t \boldsymbol{\omega}, \boldsymbol{\omega}) dt}. \]

上式 \(T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)\) 被称作 光束透射比（beam transmittance），表示光束中未被吸收或散射的光线所占的比例．\(T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)\) 有一些常用的性质．一个是

\[ T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}\right)=1, \]

另一个是

\[ T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime\prime}\right)=T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)T_{r}\left(\mathbf{p}^{\prime}\rightarrow \mathbf{p}^{\prime\prime}\right). \]

我们通常还会假设

\[ \sigma_{\mathrm{t}}(\mathbf{p},\boldsymbol{\omega})=\sigma_{\mathrm{t}}(\mathbf{p},-\boldsymbol{\omega}), \]

于是

\[ \begin{aligned} T_{r}\left(\mathbf{p}' \rightarrow \mathbf{p}\right)&=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}'+t (-\boldsymbol{\omega}), -\boldsymbol{\omega}) dt}\\ &=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+(h-t)\boldsymbol{\omega}, \boldsymbol{\omega}) dt}\\ &=\mathrm{e}^{\int_{h}^{0} \sigma_{\mathrm{t}}(\mathrm{p}+u\boldsymbol{\omega}, \boldsymbol{\omega}) du}\\ &=\mathrm{e}^{-\int_{0}^{h} \sigma_{\mathrm{t}}(\mathrm{p}+u\boldsymbol{\omega}, \boldsymbol{\omega}) du}\\ &=T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}'\right). \end{aligned} \]

特别地，如果 \(\sigma_{\mathrm{t}}\) 是常数，我们有

\[ T_{r}\left(\mathbf{p} \rightarrow \mathbf{p}^{\prime}\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}h}=\mathrm{e}^{-\sigma_{\mathrm{t}}\Vert\mathbf{p} -\mathbf{p}^{\prime}\Vert}. \]

上式被称作 Beer-Lambert 定律．

发射

点 \(\mathbf{p}\) 处的介质沿 \(\boldsymbol{\omega}\) 方向单位长度内产生的辐射率为 \(L_{\mathrm{e}}(\mathrm{p}, \omega)\)，公式写作

\[ \mathrm{d} L_{o}(\mathrm{p}, \omega)=L_{\mathrm{e}}(\mathrm{p}, \omega) \mathrm{d} t. \]

内散射

如果在点 \(\bf p\) 处，来自其他方向的光线被散射到了 \(\boldsymbol{\omega}\) 方向，则称这种散射为 内散射（in-scattering）．

我们用 相函数（phase function）\(p(\mathbf{p},\boldsymbol{\omega}_i,\boldsymbol{\omega}_o)\) 来描述散射辐射率在各个方向上的分布，其中 \(\mathbf{p}\) 是点的位置，\(\boldsymbol{\omega}_i\) 是入射光方向，\(\boldsymbol{\omega}_o\) 是散射光方向．根据定义，相函数必须满足：

\[ \int_{S^2}p(\mathbf{p},\boldsymbol{\omega}_i,\boldsymbol{\omega}_o)d\boldsymbol{\omega}_o=1. \]

内散射效应使点 \(\bf p\) 处沿 \(\boldsymbol{\omega}\) 方向出射的辐射率增加．如果考虑介质发射产生的辐射率，那么内散射和发射导致的单位长度辐射率增加的总量可以用

\[ L_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega})=L_{\mathrm{e}}(\mathbf{p},\boldsymbol{\omega})+ \int_{\mathrm{S}^{2}} p\left(\mathbf{p}, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right) \sigma_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega}_i)L_{i}\left(\mathbf{p},\boldsymbol{\omega}_i\right) d\boldsymbol{\omega}_i \]

来表示．\(L_{\mathrm{s}}(\mathbf{p},\boldsymbol{\omega})\) 通常称为 源项（source term）．

传输方程

微分-积分方程形式

设 \(\mathbf{p}(t)=\mathbf{p}_0+t\boldsymbol{\omega}\)，点 \(\mathbf{p}(t)\) 处 \(\boldsymbol{\omega}\) 方向辐射率的变化率由衰减效应和源项决定．根据这个关系得到的方程

\[ \frac{d L_{o}(\mathbf{p}(t),\boldsymbol{\omega})}{d t}=-\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})+ L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}), \]

即

\[ \begin{aligned} \frac{d L_{o}(\mathbf{p}(t),\boldsymbol{\omega})}{d t} =-&\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})+L_{\mathrm{e}}(\mathbf{p}(t),\boldsymbol{\omega}) \\ +&\int_{\mathrm{S}^{2}} p\left(\mathbf{p}(t), \boldsymbol{\omega}_i, \boldsymbol{\omega}\right) \sigma_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}_i)L_{i}\left(\mathbf{p}(t),\boldsymbol{\omega}_i\right) d\boldsymbol{\omega}_i, \end{aligned} \]

被称作 传输方程（the equation of transfer）．

积分方程形式

为了便于求解，可以通过给定边界条件

\[ L_{o}\left(\mathbf{p}(0),\boldsymbol{\omega}\right)=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right), \]

将传输方程改写为关于 \(L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})\) 的积分方程．

注意到 \(L_{o}(\mathbf{p}(t),\boldsymbol{\omega})=L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})\)，移项得

\[ \frac{d L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})}{d t}+\sigma_{t}(\mathbf{p}(t),\boldsymbol{\omega}) L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})= L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega}), \]

方程两边同乘

\[ e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du} \]

得

\[ \begin{aligned} &\frac{d L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})}{d t}e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}+ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})\frac{d\left(e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}\right)}{dt}\\ =\ & L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), -\boldsymbol{\omega}) du}, \end{aligned} \]

即

\[ d\left(L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}\right)=L_{\mathrm{s}}(\mathbf{p}(t),\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}dt. \]

从 \(0\) 积分到 \(t\) 得

\[ \left.\left(L_{i}(\mathbf{p}(s),-\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}\right)\right|_{0}^{t}=\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds \]

即

\[ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})e^{\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}-L_{i}(\mathbf{p}_0,-\boldsymbol{\omega})=\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})e^{\int_{0}^{s} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds. \]

注意到

\[ T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)=\mathrm{e}^{-\int_{0}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du} \]

方程两边同乘 \(T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)\)，移项化简得

\[ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})+\int_{0}^tL_{\mathrm{s}}(\mathbf{p}(s),\boldsymbol{\omega})\mathrm{e}^{-\int_{s}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}ds. \]

令 \(t'=t-s\)，即 \(s=t-t'\)，换元得到

\[ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})-\int_{t}^0L_{\mathrm{s}}(\mathbf{p}(t-t'),\boldsymbol{\omega})\mathrm{e}^{-\int_{t-t'}^{t} \sigma_{\mathrm{t}}(\mathbf{p}(u), \boldsymbol{\omega}) du}dt'. \]

因为 \(\mathbf{p}(t-t')=\mathbf{p}_0+t\boldsymbol{\omega}-t'\boldsymbol{\omega}=\mathbf{p}(t)-t'\boldsymbol{\omega}\)，进一步化简得

\[ L_{i}(\mathbf{p}(t),-\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}(t)\right)L_{o}(\mathbf{p}_0,\boldsymbol{\omega})+\int_{0}^tT_{r}\left( \mathbf{p}(t)-t'\boldsymbol{\omega}\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}(t)-t'\boldsymbol{\omega},\boldsymbol{\omega}\right)dt'. \]

方程

\[ L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left( \mathbf{p}-t'\boldsymbol{\omega}\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}-t'\boldsymbol{\omega},\boldsymbol{\omega}\right) \mathrm{d} t' \]

被称作传输方程的积分方程形式．令 \(\mathbf{p}^\prime=\mathbf{p}-t'\boldsymbol{\omega}\)，则传输方程也可写作

\[ L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left(\mathbf{p}^\prime\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right) \mathrm{d} t' \]

图2 - 传输方程积分示意图

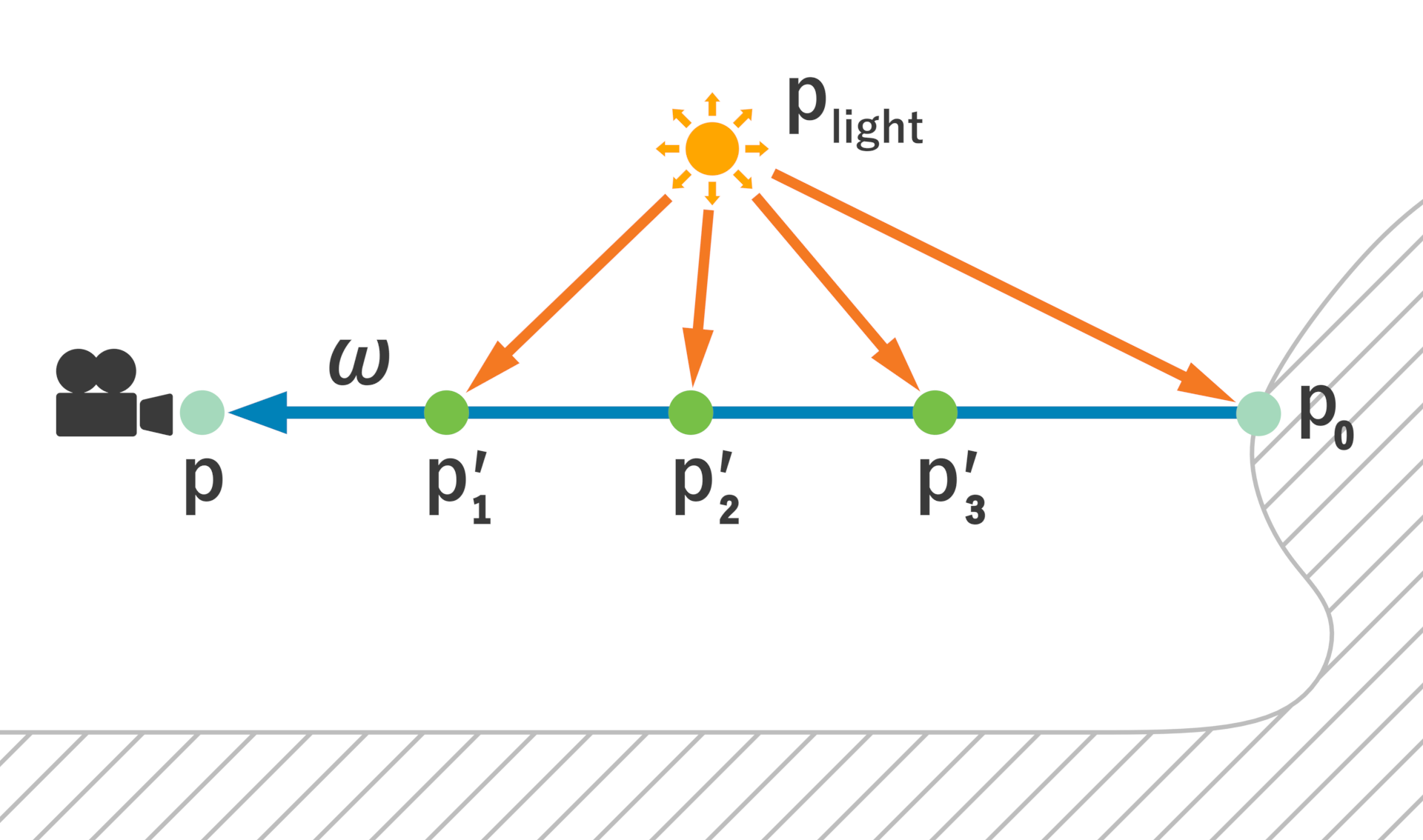
实时体积渲染

相函数

假设相函数 \(p\left(\mathbf{p}^\prime, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right)\) 只与 \(\boldsymbol{\omega}_i, \boldsymbol{\omega}\) 之间的夹角 \(\theta\) 有关，即

\[ p\left(\mathbf{p}^\prime, \boldsymbol{\omega}_i, \boldsymbol{\omega}\right)=p\left(\theta\right). \]

最简单的相函数为

\[ p\left(\theta\right)=\frac{1}{4\pi}. \]

基于物理的相函数取决于粒子的相对大小 \(s_p\)，

\[ s_{p}=\frac{2 \pi r}{\lambda}, \]

其中 \(r\) 是粒子半径，\(\lambda\) 是光的波长：

• 当 \(s_p\ll 1\)时，存在 Rayleigh 散射；

• 当 \(s_p\approx 1\)时，存在 Mie 散射；

• 当 \(s_p\gg 1\) 时，存在几何散射．

Rayleigh 散射

Rayleigh 散射的相函数为

\[ p(\theta)=\frac{3}{16 \pi}\left(1+\cos ^{2} \theta\right). \]

图3 - Rayleigh 散射相函数极坐标图像

Rayleigh 散射的散射系数与波长的四次方成反比

\[ \sigma_{s}(\lambda) \propto \frac{1}{\lambda^{4}}. \]

Mie 散射

Mie 散射的相函数

\[ p_{h g}(\theta, g)=\frac{1-g^{2}}{4 \pi\left(1+g^{2}-2 g \cos \theta\right)^{1.5}}. \]

称作 Henyey-Greenstein（HG）相函数，其中参数 \(g\in[-1,1]\)．\(g>0\) 时，发生前向散射；\(g<0\) 时，发生后向散射；\(g=0\) 时，发生各向同性散射．

Schlick 相函数

\[ p(\theta, k)=\frac{1-k^{2}}{4 \pi(1+k \cos \theta)^{2}}, \quad \text { where } \quad k \approx 1.55 g-0.55 g^{3} \]

是 HG 相函数的近似，它的计算更快．

图4 - HG 相函数（蓝色）与 Schlick 相函数（红色）极坐标图像．\(g\) 取值分别为 0，0.3，0.6

源项估计

假设介质不存在发射现象，散射系数只与位置有关，即

\[ \sigma_{\mathrm{s}}(\mathbf{p}^\prime,\boldsymbol{\omega}_i)=\sigma_{\mathrm{s}}(\mathbf{p}^\prime). \]

源项

\[ L_{\mathrm{s}}(\mathbf{p}^\prime,\boldsymbol{\omega})=\sigma_{\mathrm{s}}(\mathbf{p}^\prime)\int_{\mathrm{S}^{2}} p\left( \theta\right) L_{i}\left(\mathbf{p}^\prime,\boldsymbol{\omega}_i\right) d\boldsymbol{\omega}_i \]

可由下式进行近似计算

\[ \widehat{L}_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right)=\pi\sigma_{\mathrm{s}}(\mathbf{p}^\prime)\sum_{i=1}^{N_i} p\left( \theta\right)v\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right), \]

上式的

\[ v\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\operatorname{shadowMap}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) \cdot \operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) \]

称作可视性函数（visibility function），其中 \(\operatorname{shadowMap}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)\) 表示阴影贴图，

\[ \operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\widehat{T}_r\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right) \]

表示体积阴影．如果 \(\sigma_t(\mathbf{p})\) 是常数 \(\sigma_t\)，体积阴影的表达式为

\[ \operatorname{volshad}\left(\mathbf{p}^\prime, \mathbf{p}_{\text {light}_{i}}\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}N_j\Delta t}, \]

其中 \(N_j\Delta t\) 是从 \(\mathbf{p}^\prime\) 向 \(\mathbf{p}_{\text {light}_{i}}\) 进行光线步进得到的光线在体积中行进的距离．

源项估计式中的 \(c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)\) 是第 \(i\) 个灯光的辐射率，通常取作

\[ c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)=c_{\text {light}_{i,0}}\left(\frac{r_{0}}{ \left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|}\right)^{2}, \]

或

\[ c_{\text{light}_i}\left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|\right)=c_{\text {light}_{i,0}}\left(\frac{r_{0}}{\max \left(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|, r_{\min }\right)}\right)^{2}, \]

其中 \(c_{\text {light}_{i,0}}\) 表示 \(\left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|=r_0\) 时第 \(i\) 个灯光的辐射率．

总辐射率估计

假设衰减系数 \(\sigma_\mathrm{t}\) 只与位置有关，即

\[ \sigma_{\mathrm{t}}(\mathbf{p}^\prime,\boldsymbol{\omega}_i)=\sigma_{\mathrm{t}}(\mathbf{p}^\prime). \]

当 \(\mathbf{p}_1\) 和 \(\mathbf{p}_2\) 距离 \(\Delta t\) 较小时，我们可以用

\[ \widehat{T}_{r}\left(\mathbf{p}_1\rightarrow \mathbf{p}_2\right)=\mathrm{e}^{-\sigma_{\mathrm{t}}(\mathbf{p}_1) \Delta t} \]

作为

\[ T_{r}\left(\mathbf{p}_1\rightarrow \mathbf{p}_2\right)=\mathrm{e}^{-\int_{0}^{\Delta t} \sigma_{\mathrm{t}}(\mathbf{p}_1-u\boldsymbol{\omega}) du} \]

的估计．于是，

\[ L_{i}(\mathbf{p}, -\boldsymbol{\omega})=T_{r}\left( \mathbf{p}_{0}\rightarrow \mathbf{p}\right) L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)+\int_{0}^{t} T_{r}\left(\mathbf{p}^\prime\rightarrow \mathbf{p}\right) L_{s}\left(\mathbf{p}^\prime,\boldsymbol{\omega}\right) \mathrm{d} t' \]

的估计式可以写作

\[ \begin{aligned} \widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})&=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-S_k \Delta t} \Delta t, \end{aligned} \]

其中

\[ S_J=\sum\limits_{k=1}^{J}\sigma_{\mathrm{t}}(\mathbf{p}^\prime_k),\quad \mathbf{p}^\prime_k=\mathbf{p}-(k-1)\Delta t \boldsymbol{\omega} . \]

如果 \(\sigma_t(\mathbf{p})\) 是常数 \(\sigma_t\)，我们有更精确的估计

\[ \begin{aligned} \widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})&=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \int_{(k-1)\Delta t}^{k\Delta t}\mathrm{e}^{-\sigma_{\mathrm{t}}t'}dt'\\ &=L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\frac{1}{\sigma_{\mathrm{t}}}\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t}). \end{aligned} \]

实例

取定常数衰减系数 \(\sigma_{\mathrm{t}}\) 和各向同性相函数，辐射率的计算公式为

\[ \begin{aligned} &\widehat{L}_{i}(\mathbf{p}, -\boldsymbol{\omega})\\ =\;&L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}+\frac{1}{\sigma_{\mathrm{t}}}\sum_{k=1}^{N_k}\widehat{L}_{s}\left(\mathbf{p}^\prime_k,\boldsymbol{\omega}\right) \mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t})\\ =\;&L_{o}\left(\mathbf{p}_{0},\boldsymbol{\omega}\right)\mathrm{e}^{-S_{N_k}\Delta t}\\ &+\frac{\rho(1-\mathrm{e}^{-\sigma_{\mathrm{t}}\Delta t})}{4}\sum_{k=1}^{N_k}\mathrm{e}^{-\sigma_{\mathrm{t}}(k-1)\Delta t}\sum_{i=1}^{N_i} \frac{c_{\text {light}_{i,0}}r_{0}^2}{ \left\|\mathbf{p}^\prime-\mathbf{p}_{\text{light}_{i}}\right\|^2}\operatorname{shadowMap}\left(\mathbf{p}^\prime_k, \mathbf{p}_{\text {light}_{i}}\right)\mathrm{e}^{-\sigma_{\mathrm{t}}N_j\Delta t}. \end{aligned} \]