色彩科学

本文最后更新于：2024年5月18日 凌晨

色彩科学的研究表明，人类能感知到的所有颜色构成一个3维线性空间．只要选定一个基，我们就能将颜色编码成3维坐标．不同的编码方式，对应了不同的色彩空间．本文介绍了一些常见的色彩空间以及如何在色彩空间之间进行转换．

CIE RGB 色彩空间

定义

考虑一个离散化的光谱能量分布（Spectral Power Distribution，简称 SPD）空间，这里的光谱能量用辐射率衡量，波长范围取 \(380nm-720nm\)，波长梯度取 \(0.1nm\)．该空间是一个 \(3401\) 维的线性空间 \(\mathbb{R}^{3401}\)．在一个固定的辐射率下，一个基为：\(\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}\)．

设 \(C\) 为人类色彩映射，它将 SPD 空间的光谱能量分布映射成色觉空间 \(P\) 中的色彩．我们下面将说明：色觉空间是 \(3\) 维线性空间，色彩映射

\[ C:\mathbb{R}^{3401}\longrightarrow P \]

是一个线性映射．

首先，因为人类产生色觉的前提是视网膜收到光的刺激，所以 \(C\) 一定是满射．然后，Grassmann 定律告诉我们，色觉空间的加法可以被这样良定义：

\[ C(\mathbf{s}_1)+C(\mathbf{s}_2):=C\left(\overline{\mathbf{s}_1}+\overline{\mathbf{s}_2}\right), \]

其中 \(\overline{\mathbf{s}_1},\overline{\mathbf{s}_2}\in\mathbb{R}^{3401}\) 为满足 \(C(\overline{\mathbf{s}_1})=C(\mathbf{s}_1),C(\overline{\mathbf{s}_2})=C(\mathbf{s}_2)\) 的任意光谱能量分布．

进一步地，我们同样有良定义的数乘：对任意 \(k>0\)，对任意 \(\overline{\mathbf{s}}\in\mathbb{R}^{3401}\)，只要 \(\overline{\mathbf{s}}\) 满足 \(C(\overline{\mathbf{s}})=C(\mathbf{s})\)，就有

\[ k\,C(s):=C(k\hspace{1pt}\overline{\mathbf{s}}). \] 因此色觉空间 \(P\) 是线性空间，\(C\) 是线性映射．按照习惯，\(C(\mathbf{s})\) 将简记为 \(C\mathbf{s}\)．

我们可以还定义色觉的减法：若存在 \(\mathbf{s}_3\)，使得 \(C\mathbf{s}_1+C\mathbf{s}_3=C\mathbf{s}_2\)，则定义 \[ C\mathbf{s}_2-C\mathbf{s}_1:=C\mathbf{s}_3. \]

揭示色觉空间维数的是色匹配实验．实验结果表明：红 \(\mathbf{v}_R=C\,\mathbf{l}_{700.0}\)，绿 \(\mathbf{v}_G=C\,\mathbf{l}_{546.1}\)，蓝 \(\mathbf{v}_B=C\,\mathbf{l}_{435.8}\) 是色觉空间的一个基．换言之，任何色彩都可以表示成红、绿、蓝的线性组合．同时，红、绿、蓝中的任一种颜色都无法表示成另两种颜色的线性组合．因此，色觉空间是一个 \(3\) 维线性空间．

为了消除歧义，我们做出如下约定：色觉空间是唯一的，其中的元素就是人类能够感知到的颜色．色彩空间则有很多种，它们的集合都是 \(\mathbb{R}^3\)，不同之处在于它们配备的与色觉空间之间的双射．说得更简单一点，面对同样的一个点 \((x_1,x_2,x_3)\)，不同的色彩空间会它把解释成不同的颜色．

如果我们为色觉空间 \(P\) 选定前面所说的这个基 \(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\)，那么相应地会诱导出一个一一对应的坐标映射

\[ \mathrm{coor}_{RGB}:P\longrightarrow\mathbb{R}^3, \]

将色觉空间 \(P\) 中的颜色映射成它在这个基下的坐标．配备了这个坐标映射的 \(\mathbb{R}^3\) 就被称作 CIE RGB 色彩空间．

容易看出，色觉空间 \(P\) 每选定一个基 \(\eta\)，与之对应的坐标空间 \(\mathrm{coor}_{\mathbf{\eta}}(P)\) 就是一个色彩空间．因为坐标映射是一个线性同构，我们称这样得到的色彩空间为线性的．

坐标计算

有了基之后，我们就可以进行基于坐标的计算，把任意一个 SPD 产生的色彩用三个数进行表示．具体来说，任意 SPD \(\mathbf{s}\in\mathbb{R}^{3401}\) 产生的色彩都可由 \(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\) 进行唯一的线性表示：

\[ C\mathbf{s}=R\cdot \mathbf{v}_R+G\cdot \mathbf{v}_G+B\cdot \mathbf{v}_B. \]

即 \(C\mathbf{s}\) 拥有坐标 \((R,G,B)\). 特别地，任意单频光谱 \(\mathbf{l}_\lambda\) 产生的色彩都可由 \(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\) 进行唯一的线性表示

\[ C\,\mathbf{l}_{\lambda} =( \mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B) \begin{pmatrix} R_{\lambda} \\ G_{\lambda} \\ B_{\lambda} \end{pmatrix}. \]

设 \(C\) 在基 \(\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}\) 和基 \(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\) 下的矩阵表示为色匹配矩阵 \(CMF^{RGB}\)，则有

\[ \begin{align} (C\,\mathbf{l}_{700.0},C\,\mathbf{l}_{700.1},\cdots,C\,\mathbf{l}_{720.0})&=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)\,CMF^{RGB}\\ &=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} R_{380.0} & R_{380.1}& \cdots & R_{720.0} \\ G_{380.0} & G_{380.1}& \cdots & G_{720.0} \\ B_{380.0} & B_{380.1}& \cdots & B_{720.0} \\ \end{pmatrix}. \end{align} \]

下图即为实验确定的 CIE RGB 空间的色匹配矩阵 \(CMF^{RGB}\)．图中横坐标为 \(\lambda\) 时，红绿蓝曲线的纵坐标分别为 \(R_{\lambda},G_{\lambda},B_{\lambda}\)．


图1 - CIE 1931 RGB 色匹配函数

如果知道了色匹配矩阵 \(CMF\)，我们就能计算出任意 SPD 在色彩空间 CIE RGB 中的坐标．任给 SPD

\[ \mathbf{s}=\left(\mathbf{l}_{380.0}, \mathbf{l}_{380.1},\cdots, \mathbf{l}_{720.0}\right) \begin{pmatrix} k_{380.0} \\ k_{380.1} \\ \vdots \\ k_{720.0} \\ \end{pmatrix}, \]

我们有如下计算公式

\[ C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} R_{380.0} & R_{380.1}& \cdots & R_{720.0} \\ G_{380.0} & G_{380.1}& \cdots & G_{720.0} \\ B_{380.0} & B_{380.1}& \cdots & B_{720.0} \\ \end{pmatrix} \begin{pmatrix} k_{380.0} \\ k_{380.1} \\ \vdots \\ k_{720.0} \\ \end{pmatrix} \]

记 \(\mathbf{k}=(k_{380.0},k_{380.1},\cdots,k_{720.0})^T\)，并将 \(CMF^{RGB}\) 按行分块

\[ CMF= \begin{pmatrix} CMF^{RGB}_1 \\ CMF^{RGB}_2 \\ CMF^{RGB}_3 \end{pmatrix}, \]

计算公式可以重写为

\[ C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right) \begin{pmatrix} CMF^{RGB}_1\,\mathbf{k}\\ CMF^{RGB}_2\,\mathbf{k}\\ CMF^{RGB}_3\,\mathbf{k} \end{pmatrix}. \]

CIE rg 色度空间

色彩空间 CIE RGB 中任意一点可由三个坐标 \((R,G,B)\) 确定．映射

\[ \begin{align} r&=\frac{R}{R+G+B},\\ g&=\frac{G}{R+G+B},\\ b&=\frac{B}{R+G+B}=1-r-g. \end{align} \]

将三维的色彩空间 CIE RGB 压缩成二维的平面．下图是展示了 \((r,g)\) 构成的空间，被称作 CIE rg 色度空间．


图2 - CIE rg 色度空间

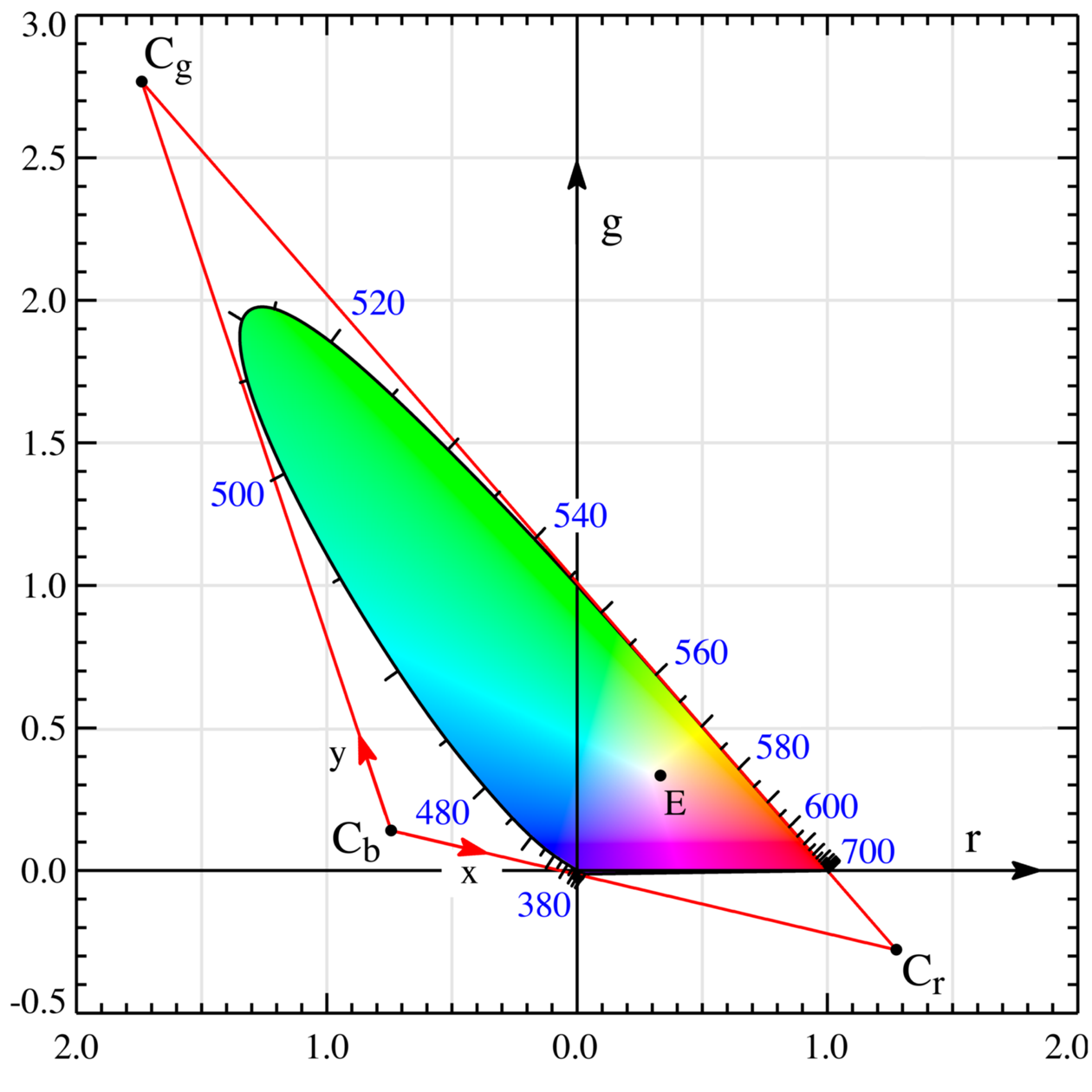
不难发现，CIE RGB 色彩空间中的任意一条直线 \(t(\hat{R},\hat{G},\hat{B})\)，在映射 \((R,G,B)\mapsto (r,g)\) 的作用下，都被压缩成 CIE rg 色度空间中的一个点 \(\left(\frac{\hat{R}}{\hat{R}+\hat{G}+\hat{B}},\frac{\hat{G}}{\hat{R}+\hat{G}+\hat{B}}\right)\)．因此，由 \((r,g)\) 表示的色度是一种与辐照度无关的属性．在这张图上，每个点具有不同的色度，但它们的辐照度完全可以被设定为相同值．

CIE XYZ 色彩空间

定义

在使用由基 \(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\) 导出的色彩空间 CIE RGB 时，有些色彩的坐标会出现负值，这在计算时不太方便．因此，我们为色觉空间更换一个更利于计算的基 \(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z\)，由此得到色彩空间 CIE XYZ．

设换基的转移矩阵为 \(T\)，我们有

\[ ( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)=(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B)T, \]

或

\[ ( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)T^{-1}=(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B), \]

因为

\[ \begin{align} (C\,\mathbf{l}_{700.0},C\,\mathbf{l}_{700.1},\cdots,C\,\mathbf{l}_{720.0})&=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)\,CMF^{RGB}\\ &=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)T^{-1}CMF^{RGB}\\ &=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)CMF^{XYZ}, \end{align} \]

所以色彩空间 CIE XYZ 的色匹配矩阵 \(CMF^{XYZ}=T^{-1}CMF^{RGB}\). 在精心选取 \(T\) 后，得到的 \(CMF^{XYZ}\) 如下图所示．


图3 - CIE 1931 XYZ 色匹配函数

从图中可以看出，色匹配矩阵 \(CMF^{XYZ}\) 的每一项都是非负的．也就是说，在色彩空间 CIE XYZ 中，单频光谱产生的色彩 \(C\,\mathbf{l}_{\lambda}\) 始终具有非负的坐标 \((X_{\lambda} , Y_{\lambda}, Z_{\lambda})\)．

亮度的表示

除了坐标分量非负，色彩空间 CIE XYZ 在表示亮度时也有着明显的优势．亮度（luminance）描述人对光明亮程度的主观感受，它与描述光的客观物理量辐射率 \(SPD(\lambda)\) 有如下关系

\[ \text{luminance}=\int_\lambda V(\lambda)SPD(\lambda)d\lambda=\sum_{i=1}^{3401}V(\lambda_i)k_{\lambda_i},\quad\lambda_i=380.0+0.1*(i-1), \]

其中 \(\lambda\) 为波长，\(V(\lambda)\) 为光度函数，\(SPD(\lambda)\) 为光谱能量分布．下图画出了实验测得的 \(V(\lambda)\)．


图4 - 光度函数

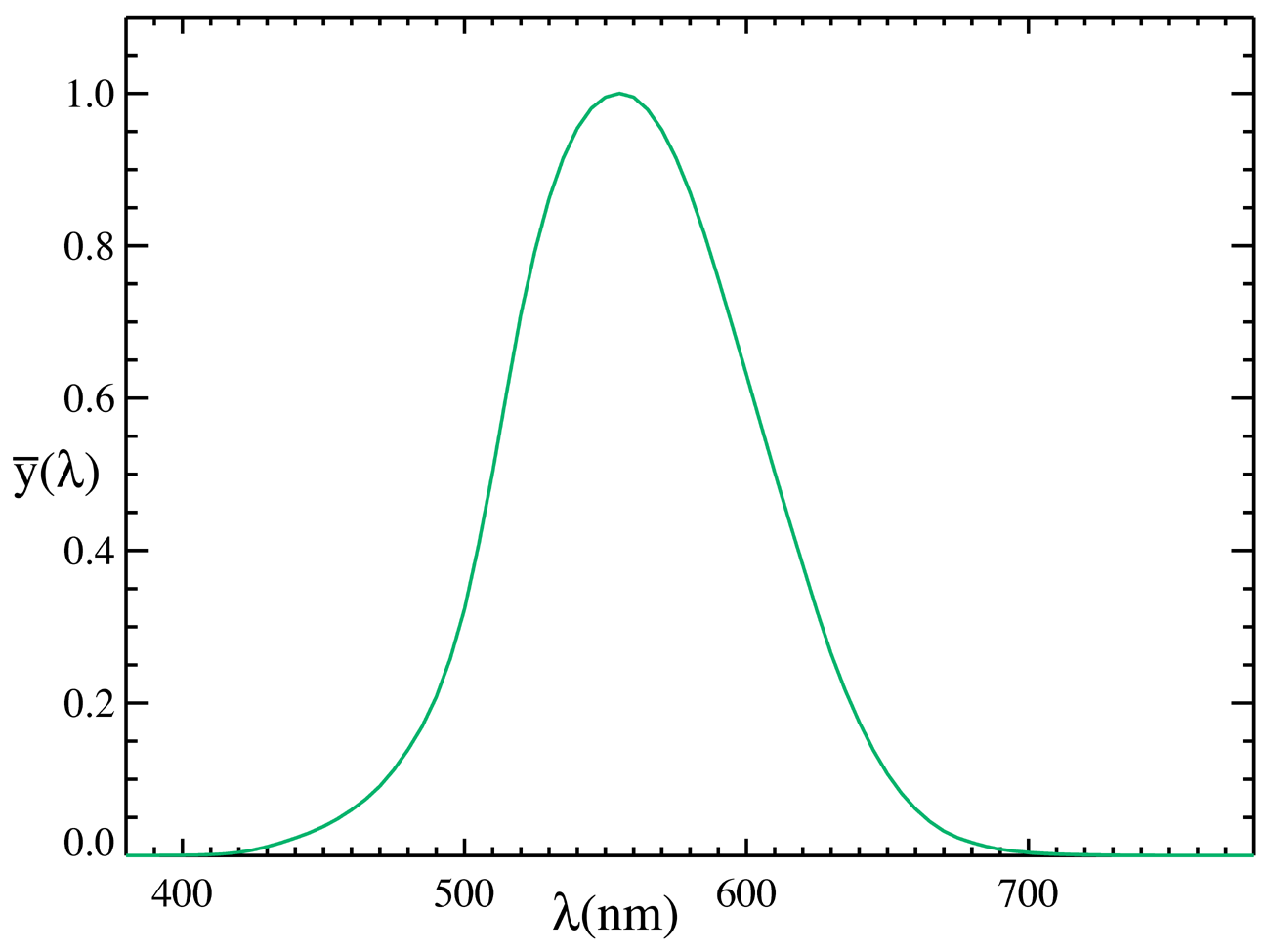
从图中可以看出，人对绿光最敏感．在辐射率相同时，绿光最亮．

事实上，色彩空间 CIE XYZ 的 \(Y\) 坐标可直接当作亮度．因为

\[ C\mathbf{s}=\left(\mathbf{v}_R,\mathbf{v}_G,\mathbf{v}_B\right)CMF^{RGB}\,\mathbf{k}=(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)CMF^{XYZ}\,\mathbf{k}. \]

设 \(C\mathbf{s}\) 在基 \(( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z)\) 下的坐标表示为

\[ C\mathbf{s}=( \mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} X \\ Y\\ Z \end{pmatrix}, \]

则有

\[ \begin{pmatrix} X \\ Y\\ Z \end{pmatrix} =CMF^{XYZ}\,\mathbf{k}. \]

设 \(CMF^{XYZ}\) 的第 \(2\) 行第 \(j\) 列的元素为 \(Y_{\lambda_j}\), 我们有 \[ Y=\sum_{j=1}^{3401}Y_{\lambda_j}\hspace{1pt}k_{\lambda_{j}} \]

因为 \(CMF^{XYZ}\) 中的绿色曲线与 \(V(\lambda)\) 曲线非常相近，可以近似认为 \(Y_{\lambda_j}=V(\lambda_j)\)，故 \(Y\) 可直接当作亮度．

xyY 空间与色度图

对 CIE XYZ 空间做非线性变换 \[ \begin{align} x&=\frac{X}{X+Y+Z},\\ y&=\frac{Y}{X+Y+Z},\\ z&=Y, \end{align} \] 就得到了一个非线性的色彩空间：xyY空间．\(x,y\) 表示色度，\(z表示明度\)．下图是一张等明度色度图，它包含了人类能看到的所有色度．


图5 - CIE 1931 xy 色度图

sRGB 色彩空间

从 CIE XYZ 空间到 sRGB 空间需要经过两步．第一步是换基，将 CIE XYZ 空间变为线性 sRGB 空间．第二步是 Gamma 变换，将线性 sRGB 空间变成最终的 sRGB 空间．

标准光源

标准光源 CIE Standard Illuminant D65 是一个相对 SPD，与辐照度无关．一方面，它在 CIE XYZ 空间中为一条直线 \(k(0.95047,1,1.08883)\)，直线上 \(Y=1\) 的点 \((0.95047,1,1.08883)\) 称为白点．另一方面，它在CIE xy 色度图中为一个点 \((0.31271,0.32902)\)．

线性 sRGB 空间

设色觉空间 \(P\) 的一个基 \((\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)\) 导出了线性 sRGB 空间． 基 \((\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)\) 是由下列条件唯一确定的：

  1. 三原色（primaries）：\(\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B\) 的 CIE xy 色度分别为 \((0.64,0.33),(0.30,0.60),(0.15,0.06)\)，即 \[ (\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B)=(\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} 0.64w_1&0.30w_2&0.15w_3\\ 0.33w_1&0.60w_2&0.06w_3\\ 0.03w_1&0.10w_2&0.79w_3 \end{pmatrix}.\]

  2. 白点：CIE XYZ 空间中的白点 \((0.95047,1,1.08883)\) 被映到 sRGB 空间中的 \((1,1,1)\)，即 \[ (\mathbf{v}_X,\mathbf{v}_Y,\mathbf{v}_Z) \begin{pmatrix} 0.95047\\ 1\\ 1.08883 \end{pmatrix} = (\mathbf{c}_R,\mathbf{c}_G,\mathbf{c}_B) \begin{pmatrix} 1\\ 1\\ 1 \end{pmatrix}. \]

联立两个条件得到

\[ \begin{pmatrix} 0.64&0.30&0.15\\ 0.33&0.60&0.06\\ 0.03&0.10&0.79 \end{pmatrix} \begin{pmatrix} w_1\\ w_2\\ w_3 \end{pmatrix} = \begin{pmatrix} 0.95047\\ 1\\ 1.08883 \end{pmatrix}. \]

解出

\[ \begin{pmatrix} w_1\\ w_2\\ w_3 \end{pmatrix} = \begin{pmatrix} 0.644463\\ 1.19192\\ 1.20292 \end{pmatrix}. \]

由此可求出 CIE XYZ 空间到线性 sRGB 空间的坐标变换公式

\[ \begin{pmatrix} R_{\text {linear }} \\ G_{\text {linear }} \\ B_{\text {linear }} \end{pmatrix}=\begin{pmatrix} +3.24096994 & -1.53738318 & -0.49861076 \\ -0.96924364 & +1.8759675 & +0.04155506 \\ +0.05563008 & -0.20397696 & +1.05697151 \end{pmatrix}\begin{pmatrix} X\\ Y \\ Z \end{pmatrix} \]

Gamma 变换

定义 Gamma 变换为

\[ \gamma(u)=\left\{\begin{array}{lll} 12.92 u & =\frac{323 u}{25} & u \leq 0.0031308 \\ 1.055 u^{1 / 2.4}-0.055 & =\frac{211 u^{\frac{5}{12}}-11}{200} & \text { otherwise } \end{array}\right. \]

它将线性 sRGB 空间中的坐标映成 sRGB 空间中的坐标，即

\[ \begin{pmatrix} R_{sRGB} \\ G_{sRGB} \\ B_{sRGB} \end{pmatrix}= \begin{pmatrix} \gamma(R_{\text {linear }})\\ \gamma(G_{\text {linear }})\\ \gamma(B_{\text {linear }}) \end{pmatrix}. \]

此外，如果有坐标分量值超出了 \(1\)，那么该分量会被钳制到 \(1\)．因为钳制的存在，从 CIE XYZ 空间到 sRGB 空间的映射并不是单射．因此，sRGB 空间能够表示的颜色是 CIE XYZ 空间的一个子集．下图展示了sRGB空间包含的色度范围．


Figure 6 - CIE 1931 xy 色域比较

扩展阅读：ACES(Academy Color Encoding System)